【题目】如图,在直角坐标平面内,直线y=-x+5与![]() 轴和
轴和![]() 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y=![]() +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.

(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且![]() ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
参考答案:
【答案】(1)、![]() ;(2)、
;(2)、![]() ;(3)、P(4,-3).
;(3)、P(4,-3).
【解析】
试题分析:(1)、根据一次函数求出A、B两点的坐标,然后代入反比例解析式进行求解;(2)、过点C作CH⊥x轴,求出CH、AH、AC、OC、OA的长度,将∠OAC转化成∠OCA,然后进行计算;(3)、过点P作PQ⊥x轴并延长角直线于点Q,设出点P和点Q的坐标,求出PQ的长度,根据三角形的面积关系列出方程,然后进行求解,根据点P在x轴下方进行舍根.
试题解析:(1)、由直线y=-x+5得点B(0,5),A(5,0),将A、B两点的坐标代入![]() ,
,
得 ![]() ,解得
,解得![]() ∴抛物线的解析式为
∴抛物线的解析式为![]()
(2)、过点C作CH⊥x轴交x轴于点H 把![]() 配方得
配方得![]() ∴点C(3,-4),
∴点C(3,-4),
∴CH=4,AH=2,AC=![]() ∴OC=5, ∵OA=5 ∴OA=OC ∴∠OAC=∠OCA
∴OC=5, ∵OA=5 ∴OA=OC ∴∠OAC=∠OCA
sin∠OCA=sin∠OAC=![]()
(3)、过P点作PQ![]() x轴并延长交直线y=-x+5于Q
x轴并延长交直线y=-x+5于Q
设点P(m,![]() -6m+5),Q(m,-m+5) ∴PQ=-m+5-(
-6m+5),Q(m,-m+5) ∴PQ=-m+5-(![]() -6m+5)=-
-6m+5)=-![]() +5m
+5m
∵![]()
∴![]()
∴![]() ∴
∴![]()
∴P(1,0)(舍去),P(4,-3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列调查中,适宜采用普查的是( )
A.了解我省中学生的视力情况
B.了解八(1)班学生校服的尺码情况
C.检测一批炮弹的杀伤半径
D.调查电视剧《人民的名义》的收视率 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解我校八年级学生的视力情况,从八年级全部960名学生中随机抽查了80名学生的视力.在这个问题中,样本的容量是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确有( )个。

A.2个 B.3个 C.4个 D.5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】“平行四边形的对角线互相垂直”是事件.(填“必然”、“随机”、“不可能”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
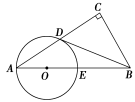
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB与A′B′分别是☉O与☉O′的两条弦,AB=A′B′,那么∠AOB与∠A′O′B′的大小关系是( )
A. ∠AOB=∠A′O′B′ B. ∠AOB>∠A′O′B′ C. ∠AOB<∠A′O′B′ D. 不能确定
相关试题

