【题目】如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE= ![]() ,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为 .
,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为 . 
参考答案:
【答案】3
【解析】解:
∵四边形ABCD为矩形,且AE⊥BD,tan∠BAE= ![]() ,BE=1,
,BE=1,
∴AB=2,AE= ![]() ,
,
∵tan∠BAE= ![]() ,
,
∴∠BAE=30°,
∴∠EAD=60°,
∵AE= ![]() ,
,
∴DE=3,
如图,设A点关于BD的对称点为A′,连接A′D,PA′,

则A′A=2AE=2 ![]() ,AD=A′D=2
,AD=A′D=2 ![]() ,
,
∴△AA′D是等边三角形,
∵PA=PA′,
∴当A′、P、Q三点在一条线上时,A′P+PQ最小,
又垂线段最短可知当PQ⊥AD时,A′P+PQ最小,
∴AP+PQ=A′P+PQ=A′Q=DE= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解轴对称-最短路线问题(已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线y=x2﹣4x+2﹣t(t为实数)在0<x<
 的范围内与x轴有公共点,则t的取值范围为( )
的范围内与x轴有公共点,则t的取值范围为( )
A.﹣2<t<2
B.﹣2≤t<2
C.﹣ <t<2
<t<2
D.t≥﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 轴,
轴,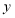 轴分别交于
轴分别交于 ,
, 两点,且经过点
两点,且经过点 .
.(1)求
 的值;
的值;(2)若
 ,
,①求
 的值;
的值;②点
 为
为 轴上一动点,点
轴上一动点,点 为坐标平面内另一点,若以
为坐标平面内另一点,若以 ,
, ,
, ,
, 为顶点的四边形是菱形,请直接写出所有符合条件的点
为顶点的四边形是菱形,请直接写出所有符合条件的点 的坐标.
的坐标.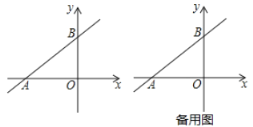
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, ,AD是
,AD是 的高,
的高, ,
, ,垂足分别为E、F,
,垂足分别为E、F, 图中有哪些全等的三角形?
图中有哪些全等的三角形? 请一一写出,不需要说明理由
请一一写出,不需要说明理由
 说明
说明 与
与 全等的理由.
全等的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
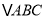 中,
中, ,
, ,D是AC的中点,E是BC延长线上的一点,且
,D是AC的中点,E是BC延长线上的一点,且 ,
, ,垂足为M.
,垂足为M.
 求
求 的度数;
的度数; 求证:M是BE的中点.
求证:M是BE的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,对其份数和成绩(十分制)进行整理,制成了如下两幅不完整的统计图.

(1)求本次抽取的作品数量并补全条形统计图;
(2)此次被抽取的作品的平均得分是分.
(3)若该校共征集到800份作品,请估计8分的作品约有多少份? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.

相关试题

