【题目】如图，直线与轴，轴分别交于，两点，且经过点．

（1）求的值；

（2）若，

①求的值；

②点为轴上一动点，点为坐标平面内另一点，若以，，，为顶点的四边形是菱形，请直接写出所有符合条件的点的坐标．

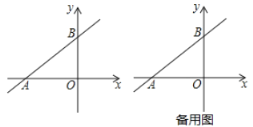
参考答案：

【答案】（1）；（2）①3；②或或或．

【解析】

（1）将点(4,b+3)代入直线解析式中即可得出结论;
（2）①先求出点A,B坐标,进而得出AB，再利用AB=OB+2，即可求出b;
②分三种情况利用菱形的性质即可得出结论．

解:(1)直线y=kx+b经过点(4，b+3)
∴4k+b=b+3,
∴4k=3,
∴k=

（2）①由（1）知A,B在y=x+b上，

当x=0时，y=b, ∴B(0,b)，

当y=0时，x+b=0，解得x= ∴A(,0)，

∴OA=，OB=b

∴AB=

∵AB=OB+2

∴=b+2

∴b=3

故答案为：3

②如图，由①知，b=3，∴A(-4,0)，B(0,3) ∴AB=5

∵以A,B,M,N为顶点的四边形是菱形，

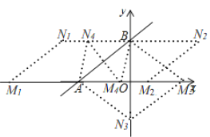
所以，分3种情况：

Ⅰ、当AB与AM为两邻边时，BN∥AM，BN=AM=AB=5，

∴N(-5,3)或(5,3)

Ⅱ、当AB与BM为两邻边时，AM和AN是对角线，∵B(0,3) ∴N(0,-3)，

Ⅲ、当AM和AN为两邻边时，BN∥AM，

设N(n,3)，∴BM=AM=BN=﹣n ∴OM=4+n，

根据勾股定理得，n2-(4+n)2=9,
n=﹣
N(﹣,3)

故答案为：N(5,3)或(-5,3)或(0,-3)或(﹣,3)

关闭