【题目】已知:E是∠AOB的平分线上一点,EC⊥OA ,ED⊥OB ,垂足分别为C、D求证:(1)△OED≌△OEC (2)∠ECD=∠EDC

参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)由OE平分∠AOB可得∠AOE=∠BOE,由EC⊥OA,ED⊥OB可得∠OCE=∠ODE=90°,从而根据“AAS”可证明△OED≌△OEC;
(2)由角平分线的性质可得EC=DE,从而可证∠ECD=∠EDC.
(1)证明∵OE平分∠AOB,
∴∠AOE=∠BOE.
∵EC⊥OA,ED⊥OB,
∴∠OCE=∠ODE=90°.
又∵OE=OE,
∴△OED≌△OEC(AAS);
(2)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=DE,
∴∠ECD=∠EDC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解在数轴上表示为( )
的解在数轴上表示为( )
A.
B.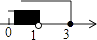
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平面直角坐标系中,点A、B的坐标分别是(a,0),(b,0)且
 +|b-2|=0.
+|b-2|=0.
(1)求a、b的值;
(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.
(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿平行于x轴的负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,那么关于此二次函数的下列四个结论:①a+b+c<0;②c>1;③b2﹣4ac>0;④2a﹣b<0,其中正确的结论有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
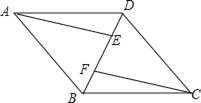
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=﹣2x﹣3与y2=
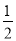 x+2.
x+2.(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>
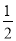 x+2的解集为多少?
x+2的解集为多少?(3)求两图象和y轴围成的三角形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场柜台销售每台进价分别为160元、120元的
 、
、 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:销售时段
销售数量
销售收入
 种型号
种型号 种型号
种型号第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求
 、
、 两种型号的电器的销售单价;
两种型号的电器的销售单价;(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求
 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
相关试题

