【题目】某商场柜台销售每台进价分别为160元、120元的![]() 、
、![]() 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求![]() 、
、![]() 两种型号的电器的销售单价;
两种型号的电器的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求![]() 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?
(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)A型电器销售单价为200元,B型电器销售单价150元;(2)最多能采购37台;(3)方案一:采购A型36台B型14台;方案二:采购A型37台B型13台.
【解析】
(1)设A、B两种型号电器的销售单价分别为x元、y元,根据3台A型号4台B型号的电器收入1200元,5台A型号6台B型号的电器收入1900元,列方程组求解;
(2)设采购A种型号电器a台,则采购B种型号电器(50a)台,根据金额不多余7500元,列不等式求解;
(3)根据A型号的电器的进价和售价,B型号的电器的进价和售价,再根据一件的利润乘以总的件数等于总利润列出不等式,再进行求解即可得出答案.
解:(1)设A型电器销售单价为x元,B型电器销售单价y元,
则![]() ,
,
解得:![]() ,
,
答:A型电器销售单价为200元,B型电器销售单价150元;
(2)设A型电器采购a台,
则160a+120(50a)≤7500,
解得:a≤![]() ,
,
则最多能采购37台;
(3)设A型电器采购a台,
依题意,得:(200160)a+(150120)(50a)>1850,
解得:a>35,
则35<a≤![]() ,
,
∵a是正整数,
∴a=36或37,
方案一:采购A型36台B型14台;
方案二:采购A型37台B型13台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:E是∠AOB的平分线上一点,EC⊥OA ,ED⊥OB ,垂足分别为C、D求证:(1)△OED≌△OEC (2)∠ECD=∠EDC

-
科目: 来源: 题型:
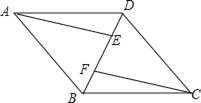
查看答案和解析>>【题目】已知:如图,四边形ABCD是平行四边形,AE∥CF,且分别交对角线BD于点E,F.
(1)求证:△AEB≌△CFD;
(2)连接AF,CE,若∠AFE=∠CFE,求证:四边形AFCE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=﹣2x﹣3与y2=
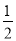 x+2.
x+2.(1)在同一平面直角坐标系中,画出这两个函数的图象;
(2)根据图象,不等式﹣2x﹣3>
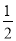 x+2的解集为多少?
x+2的解集为多少?(3)求两图象和y轴围成的三角形的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
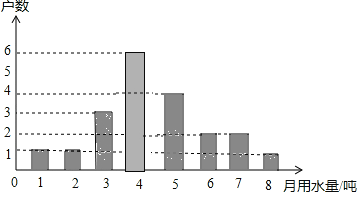
(1)小明一共调查了多少户家庭?
(2)求所调查家庭3月份用水量的众数、中位数和平均数;
(3)若该小区有800户居民,请你估计这个小区3月份的总用水量是多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图1,直线
 、
、 、
、 两两相交,交点分别为点A、B、C,点D在线段
两两相交,交点分别为点A、B、C,点D在线段 上,过点D作
上,过点D作 交
交 于点E,过点E作
于点E,过点E作 交
交 于点F.若
于点F.若 ,求
,求 的度数.请将下面的解答过程补充完整,并填空
的度数.请将下面的解答过程补充完整,并填空解:∵
 ,∴
,∴ ________.( )
________.( )∵
 ,∴________
,∴________ ( )
( )∴
 .(等量代换)
.(等量代换)∵
 ,∴
,∴ ________°.
________°.应用:如图2,直线
 、
、 、
、 两两相交,交点分别为点A、B、C,点D在线段
两两相交,交点分别为点A、B、C,点D在线段 的延长线上,过点D作
的延长线上,过点D作 交
交 于点E,过点E作
于点E,过点E作 交
交 于点F.若
于点F.若 ,求
,求 的度数,并仿照(1)进行说明.
的度数,并仿照(1)进行说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对,正确处置,顺利返航,避免了一场灾难的发生,创造了世界航空史上的奇迹!下表给出了距离地面高度与所在位置的温度之间的大致关系.根据下表,请回答以下几个问题:
距离地面高度(千米)
0
1
2
3
4
5
所在位置的温度(℃)
20
14
8
2
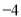
(1)上表反映的两个变量中,______是自变量,______是因变量.
(2)若用h表示距离地面的高度,用y表示表示温度,则y与h的之间的关系式是:__________;
当距离地面高度5千米时,所在位置的温度为:_________℃.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用时间关系图.根据图象回答以下问题:
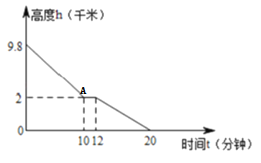
(3)点A表示的意义是什么?返回途中飞机在2千米高空水平大约盘旋了几分钟?
(4)飞机发生事故时所在高空的温度是多少?
相关试题

