【题目】在Rt△ABC中,∠B=90°,AB=8,CB=5,动点M从C点开始沿CB运动,动点N从B点开始沿BA运动,同时出发,两点均以1个单位/秒的速度匀速运动(当M运动到B点即同时停止),运动时间为t秒.
(1)AN= ;CM= .(用含t的代数式表示)
(2)连接CN,AM交于点P.
①当t为何值时,△CPM和△APN的面积相等?请说明理由.
②当t=3时,试求∠APN的度数.

参考答案:
【答案】(1)8﹣t,t;(2)①![]() ;②∠APN=45°
;②∠APN=45°
【解析】
(1)根据路程=速度×时间,可用含t的代数式表示BN,CM的长,即可用含t的代数式表示AN的长;
(2)①由题意可得S△ABM=S△BNC,根据三角形面积公式可求t的值;
②过点P作PF⊥BC,PG⊥AB,过点A作AE⊥CN,交CN的延长线于点E,连接BP,可证四边形PGBF是矩形,可得PF=BG,根据三角形的面积公式,可得方程组,求出PG,PF的长,根据勾股定理可求PN的长,通过证△ANE∽△CNB,可求AE,NE的长,即可求∠APN的度数.
解:(1)∵M,N两点均以1个单位/秒的速度匀速运动,
∴CM=BN=t,
∴AN=8﹣t,
故答案为:8﹣t,t;
(2)①若△CPM和△APN的面积相等
∴S△CPM+S四边形BMPN=S△APN+S四边形BMPN,
∴S△ABM=S△BNC,
∴![]() ,
,
∴8×(5﹣t)=5t
∴t=![]()
∴当t=![]() 时,△CPM和△APN的面积相等;
时,△CPM和△APN的面积相等;
②如图,过点P作PF⊥BC,PG⊥AB,过点A作AE⊥CN,交CN的延长线于点E,连接BP,

∵PG⊥AB,PF⊥BC,∠B=90°,
∴四边形PGBF是矩形,
∴PF=BG,
∵t=3,
∴CM=3=BN,
∴BM=2,AN=5,
∵S△ABM=S△ABP+S△BPM,
∴![]()
∴16=8PG+2PF①
∵S△BCN=S△BCP+S△BPN,
∴![]() ×5×3=
×5×3=![]()
∴15=3PG+5PF②
由①②组成方程组解得:PG=![]() ,PF=
,PF=![]() ,
,
∴BG=![]()
∴NG=BN﹣BG=3﹣![]() =
=![]()
在Rt△PGN中,PN=![]() =
=![]() ,
,
在Rt△BCN中,CN=![]() =
=![]()
∵∠B=∠E=90°,∠ANE=∠BNC
∴△ANE∽△CNB
∴![]()
∴![]()
∴AE=![]() ,NE=
,NE=![]()
∵PE=EN+PN
∴PE=![]() +
+![]() =
=![]()
∴AE=PE,且AE⊥PE
∴∠APN=45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
-
科目: 来源: 题型:
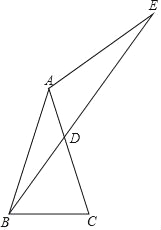
查看答案和解析>>【题目】如图,已知△ABC中AB=AC,在AC上有一点D,连接BD,并延长至点E,使AE=AB.
(1)画图:作∠EAC的平分线AF,AF交DE于点F(用尺规作图,保留作图痕迹,不写作法);
(2)在(1)的条件下,连接CF,求证:∠ABE=∠ACF;
(3)若AC=8,∠E=15°,求三角形ABE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
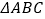 中,
中,  ,tan
,tan  ,AB=6cm.动点P从点A开始沿边AB向点B以1 cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,
,AB=6cm.动点P从点A开始沿边AB向点B以1 cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,  的最大面积是( )
的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;②AB=DE,∠B=∠E.BC=EF;③∠B=∠E,BC=EF,∠C=∠F;④AB=DE,AC=DF,∠B=∠E. 其中,能使△ABC≌△DEF 的条件共有( )

A. 1 组B. 2 组C. 3 组D. 4 组
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与
与 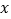 轴、
轴、  轴分别交于点A、B,点C在X轴上,
轴分别交于点A、B,点C在X轴上,  ,则点C的坐标是( )
,则点C的坐标是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC 是等边三角形,P 是 BC 上任意一点,PD⊥AB,PE⊥AC,连接 DE.记△ADE 的周长为
 ,四边形 BDEC 的周长为
,四边形 BDEC 的周长为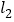 ,则
,则 与
与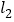 的大小关系是( )
的大小关系是( )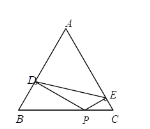
A.
 =
=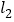 B.
B.  >
>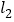 C.
C.  <
<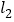 D. 无法确定
D. 无法确定
相关试题

