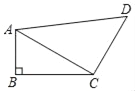
【题目】如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据直角三角形的性质得到AC=2AB=4,根据跟勾股定理的逆定理即可得到结论;
(2)根据勾股定理得到BC![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
(1)在Rt△ABC中,∠B=90°,∠ACB=30°,AB=2,∴AC=2AB=4.在△ACD中,AC=4,CD=3,AD=5.
∵42+32=52,即AC2+CD2=AD2,∴∠ACD=90°,∴AC⊥CD;
(2)在Rt△ABC中,∠B=90°,AB=2,AC=4,∴BC![]() ,∴Rt△ABC的面积为
,∴Rt△ABC的面积为![]() ABBC
ABBC![]() 2×2
2×2![]() .
.
又∵Rt△ACD的面积为![]() ACCD
ACCD![]() 4×3=6,∴四边形ABCD的面积为:2
4×3=6,∴四边形ABCD的面积为:2![]() 6.
6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温州某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至于30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿? -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小芸设计的“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:①以点A为圆心,适当长为半径画弧,
交直线BC于点M,N;
②分别以点M,N为圆心,以大于
 MN的长为半径画弧,两弧相交于点P;
MN的长为半径画弧,两弧相交于点P;③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵AM= ,MP= ,
∴AP是线段MN的垂直平分线.( )(填推理的依据)
∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
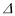 ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,
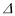 PEC 与
PEC 与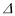 QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;(2)请问:当 x 3 时,
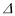 PEC 与
PEC 与 QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
-
科目: 来源: 题型:
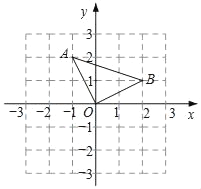
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点O(0,0),A(﹣1,2),B(2,1).
(1)在图中画出△AOB关于y轴对称的△A1OB1,并直接写出点A1和点B1的坐标;(不写画法,保留画图痕迹)
(2)在x轴上存在点P,使得PA+PB的值最小,则点P的坐标为 ,PA+PB的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在第一个
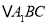 中,
中,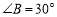 ,
,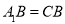 ,在边
,在边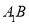 上任取一
上任取一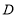 ,延长
,延长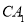 到
到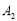 ,使
,使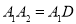 ,得到第
,得到第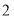 个
个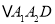 ,在边
,在边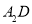 上任取一点
上任取一点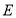 ,延长
,延长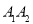 到
到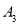 ,使
,使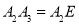 ,得到第三个
,得到第三个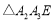 ,…按此做法继续下去,第
,…按此做法继续下去,第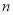 个等腰三角形的底角的度数是________________.
个等腰三角形的底角的度数是________________.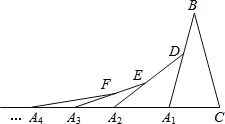
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.
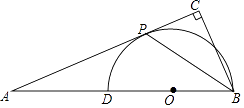
(1)求证:BP平分∠ABC;
(2)若PC=1,AP=3,求BC的长.
相关试题

