【题目】如图,在矩形ABCD中,AB=6,BC=8,动点Q从点A出发,沿着AB方向以1个单位长度/秒的速度匀速运动,同时动点P从点B出发,沿着对角线BD方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5),以P为圆心,PB长为半径的⊙P与BD、AB的另一个交点分别为E、F,连结EF、QE. 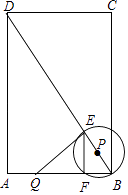
(1)填空:FB=(用t的代数式表示);
(2)当t为何值时,点Q与点F相遇?
(3)当线段QE与⊙P有两个公共点时,求t的取值范围.
参考答案:
【答案】
(1)![]() t
t
(2)解:当点Q与点F相遇时,AQ+BF=AB,
∴t+ ![]() t=6,
t=6,
∴t= ![]() s,
s,
∴当t= ![]() s时,点Q与点F相遇
s时,点Q与点F相遇
(3)解:当直线QE与⊙P相切时,
∵∠BEQ=∠A=90°,∠QBE=∠ABD,
∴△QBE∽△DBA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() s,
s,
∵线段QE与⊙P有两个公共点,
∴t的取值范围: ![]() <t<
<t< ![]() .
.
【解析】解:(1)∵BE是⊙P的直径,四边形ABCD是矩形, ∴∠EFB=∠A=90°
在Rt△ABC中,∵AD=8,AB=6,
∴BD= ![]() =10,
=10,
∵EF∥AD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BF= ![]() t.
t.
给答案为 ![]() t.
t.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的条件是( )
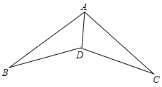
A. ∠B=∠C,BD=DC B. ∠ADB=∠ADC,BD=DC
C. ∠B=∠C,∠BAD=∠CAD D. BD=DC,AB=AC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.BE与DF之间有怎样的关系?请说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径总长度为( )

A.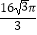
B.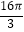
C.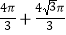
D.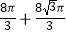
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形均是一些科技创新公司标志图,其中既是中心对称图形又是轴对称图形的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图①,在△ABC 中,D、E 分别是 AB、AC 上的点,AB=AC,AD=AE,然后将△ADE 绕点 A 顺时针旋转一定角度,连接 BD,CE,得到图②,将 BD、CE 分别延长至 M、N,使 DM=
 BD,EN=
BD,EN= CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:(1)在图②中,BD 与 CE 的数量关系是 ;
(2)在图③中,猜想 AM 与 AN 的数量关系,∠MAN 与∠BAC 的数量关系,并证明你的猜想.

相关试题

