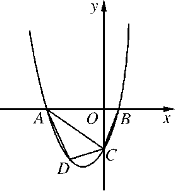
【题目】已知,如图,抛物线![]() >0)与
>0)与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)、![]() ;(2)、
;(2)、![]() ;(3)、P1(-2,-3),
;(3)、P1(-2,-3),![]() ,
,![]()
【解析】
试题分析:(1)、根据题意得出点B和点C的坐标,然后代入函数解析式求出答案;(2)、首先根据点A和点C的坐标得出直线AC的解析式,然后过点D作DM∥y轴分别交线段AC和x轴于点M,N,设点M的坐标为(m,-m-3),从而得出点D的坐标,求出DM的长度,根据二次函数的性质求出DM的最大值,得出面积的最大值;(3)、①、过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,,将C(0,-3)代入函数解析式求出点P的坐标;②、平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,设出点P的坐标为(x,3),然后代入函数解析式求出点P的坐标.
试题解析:(1)、∵OC=3OB,B(1,0),∴C(0,-3). 把点B,C的坐标代入![]() ,得
,得![]()
∴抛物线的解析式![]()
(2)、由A(-3,0),C(0,-3)得直线AC的解析式为![]() ,
,
如图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
设M![]() 则D
则D![]() ,
,![]()
∴-1<0,∴当x=![]() 时,DM有最大值
时,DM有最大值![]() ∴S四边形ABCD=S△ABC+S△ACD
∴S四边形ABCD=S△ABC+S△ACD![]()
此时四边形ABCD面积有最大值为![]() .
.
(3)、存在
①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1,
此时四边形ACP1E1为平行四边形. ∵C(0,-3),令![]()
∴![]() ,
,![]() .∴P1(-2,-3).
.∴P1(-2,-3).
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,∵C(0,-3),
∴可令P(x,3),![]() ,得
,得![]() 解得
解得![]() ,
,![]()
此时存在点![]() ,
,![]()
综上所述,存在3个点符合题意,坐标分别是P1(-2,-3),![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】太原冬季某日的最高气温是3℃,最低气温为﹣12℃,那么当天的温差是_____℃.
-
科目: 来源: 题型:
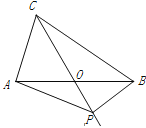
查看答案和解析>>【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组等式,
第1个等式:22﹣12=2+1,
第2个等式:32﹣22=3+2,
第3个等式:42﹣32=4+3.
…
根据上述等式的规律,第n个等式用含n的式子表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:7ab﹣3(a2﹣2ab)﹣5(4ab﹣a2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值:x2﹣2(x2﹣3xy)+3(y2﹣2xy)﹣2y2,其中x=
 ,y=﹣1;
,y=﹣1;(2)已知x+y=6,xy=﹣1,求代数式2(x+1)﹣(3xy﹣2y)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数
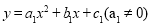 与
与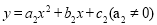 满足
满足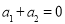 ,
,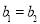 ,
,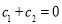 ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.求函数
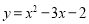 的“旋转函数”.
的“旋转函数”.小明是这样思考的:由函数
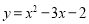 可知,
可知,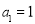 ,
,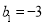 ,
,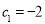 ,根据
,根据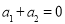 ,
,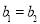 ,
,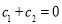 ,求出
,求出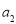 ,
,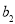 ,
,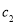 ,就能确定这个函数的“旋转函数”.
,就能确定这个函数的“旋转函数”.请参考小明的方法解决下面问题:
(1)直接写出函数
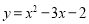 的“旋转函数”;
的“旋转函数”;(2)若函数
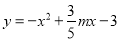 与
与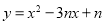 互为“旋转函数”,求
互为“旋转函数”,求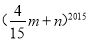 的值;
的值;(3)已知函数
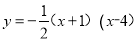 的图象与
的图象与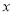 轴交于点A、B两点(A在B的左边),与
轴交于点A、B两点(A在B的左边),与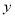 轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数
轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数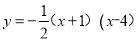 互为“旋转函数”。
互为“旋转函数”。
相关试题

