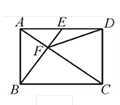
【题目】如图,在矩形ABCD中,AB=3,BE⊥AC于点F,交边AD于点E,连结DF,若点E为AD的中点,则DF的长为__________ .
参考答案:
【答案】3
【解析】分析:过F作FH⊥AD于H.设AE=x,则ED=x.由∠1=∠3,得到tan∠1=![]() =
=![]() =tan∠3=
=tan∠3=![]() =
=![]() ,解方程得到AE的长.由勾股定理得到BE的长.由S△ABE=
,解方程得到AE的长.由勾股定理得到BE的长.由S△ABE=![]() AB×AE=
AB×AE=![]() EB×AF,得到AF的长.再由∠1=∠3,得到sin∠1=sin∠3,从而得到FH、AH、HD的长,即可得到结论.
EB×AF,得到AF的长.再由∠1=∠3,得到sin∠1=sin∠3,从而得到FH、AH、HD的长,即可得到结论.
详解:过F作FH⊥AD于H.设AE=x,则ED=x.
∵∠BAC=90°,∴∠2+∠3=90°.
∵BE⊥AC,∴∠1+∠2=90°,∴∠1=∠3.在Rt△ABE中,tan∠1=![]() =
=![]() .在Rt△ADC中,tan∠3=
.在Rt△ADC中,tan∠3=![]() =
=![]() ,∴
,∴![]() =
=![]() ,解得:x=
,解得:x=![]() (负数舍去).在Rt△ABE中,BE=
(负数舍去).在Rt△ABE中,BE=![]() =
=![]() .
.
∵S△ABE=![]() AB×AE=
AB×AE=![]() EB×AF,∴
EB×AF,∴![]() ,解得:AF=
,解得:AF=![]() .
.
∵∠1=∠3,∴sin∠1=sin∠3,∴![]() ,解得:FH=1,∴AH=
,解得:FH=1,∴AH=![]() =
=![]() =
=![]() ,∴HD=AD-AH=
,∴HD=AD-AH=![]() =
=![]() ,∴FD=
,∴FD=![]() =
=![]() =3.
=3.
故答案为:3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
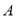 在数轴上对应的数为
在数轴上对应的数为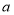 ,点
,点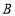 对应的数为
对应的数为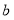 ,
,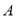 与
与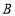 之间的距离记作AB.
之间的距离记作AB.
已知a=-2,b比a大12,(1)则B点表示的数是_____;
(2)设点
 在数轴上对应的数为
在数轴上对应的数为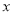 ,当PA-PB=4时,求
,当PA-PB=4时,求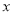 的值;
的值;(3)若点M以每秒1个单位的速度从A点出发向右运动,同时点N以每秒2个单位的速度从B点向左运动。设运动时间是t秒,则运动t秒后,
用含t的代数式表示M点到达的位置表示的数为_____, N点到达的位置表示的数为_____;
当t为多少秒时,M与N之间的距离是9?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,BE⊥AC于点E,点F是AB的中点, AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;② AH=2BD; ③AD·BC=AE·AB; ④2CD2=
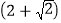 EH2.其中正确的结论有( )
EH2.其中正确的结论有( )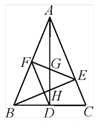
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车一天上午从省实验中学门口出发沿着南北向的文化路营运,向北为正,向南为负,行驶里程(单位:
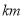 )依次顺序记录如下:+18,-5,-2,+3,+10,-9,+12,-3,-7,-15.
)依次顺序记录如下:+18,-5,-2,+3,+10,-9,+12,-3,-7,-15.(1)将最后一名乘客送到目的地,出租车在出发地什么方向?距离出发地多远?
(2)不超过3千米时,按照步价收费8元,超过3千米的部分,每千米1.5元,司机上午的营业额是多少?
-
科目: 来源: 题型:
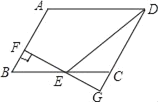
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=_____.
-
科目: 来源: 题型:
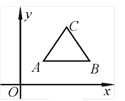
查看答案和解析>>【题目】如图,等边三角形ABC的顶点A、B坐标分别为(1,1)、(3,1),若把等边△ABC先沿x轴翻折,再向左平移1个单位”为第一次変换,则这样连续经过2017次变换后,等边△ABC的顶点C的坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于
 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )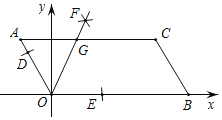
A. (
 ﹣1,2) B. (
﹣1,2) B. ( ,2) C. (3﹣
,2) C. (3﹣ ,2) D. (
,2) D. ( ﹣2,2)
﹣2,2)
相关试题

