【题目】已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣![]() x+b与抛物线的另一个交点为D.
x+b与抛物线的另一个交点为D.
(1)若点D的横坐标为2,求抛物线的函数解析式;
(2)若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;
(3)在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒![]() 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
参考答案:
【答案】(1) y=﹣![]() x2﹣2
x2﹣2![]() x+3
x+3![]() ;(2) P的坐标为(﹣4,﹣
;(2) P的坐标为(﹣4,﹣![]() )和(﹣6,﹣
)和(﹣6,﹣![]() );(3) (1,﹣4
);(3) (1,﹣4![]() ).
).
【解析】
试题分析:(1)根据二次函数的交点式确定点A、B的坐标,求出直线的解析式,求出点D的坐标,求出抛物线的解析式;(2)作PH⊥x轴于H,设点P的坐标为(m,n),分△BPA∽△ABC和△PBA∽△ABC,根据相似三角形的性质计算即可;(3)作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,根据正切的定义求出Q的运动时间t=BE+EF时,t最小即可.
试题解析:(1)∵y=a(x+3)(x﹣1),
∴点A的坐标为(﹣3,0)、点B两的坐标为(1,0),
∵直线y=﹣![]() x+b经过点A,
x+b经过点A,
∴b=﹣3![]() ,
,
∴y=﹣![]() x﹣3
x﹣3![]() ,
,
当x=2时,y=﹣5![]() ,
,
则点D的坐标为(2,﹣5![]() ),
),
∵点D在抛物线上,
∴a(2+3)(2﹣1)=﹣5![]() ,
,
解得,a=﹣![]() ,
,
则抛物线的解析式为y=﹣![]() (x+3)(x﹣1)=﹣
(x+3)(x﹣1)=﹣![]() x2﹣2
x2﹣2![]() x+3
x+3![]() ;
;
(2)作PH⊥x轴于H,
设点P的坐标为(m,n),
当△BPA∽△ABC时,∠BAC=∠PBA,
∴tan∠BAC=tan∠PBA,即![]() =
=![]() ,
,
∴![]() =
=![]() ,即n=﹣a(m﹣1),
,即n=﹣a(m﹣1),
∴![]() ,
,
解得,m1=﹣4,m2=1(不合题意,舍去),
当m=﹣4时,n=5a,
∵△BPA∽△ABC,
∴![]() =
=![]() ,即AB2=ACPB,
,即AB2=ACPB,
∴42=![]()
![]() ,
,
解得,a1=![]() (不合题意,舍去),a2=﹣
(不合题意,舍去),a2=﹣![]() ,
,
则n=5a=﹣![]() ,
,
∴点P的坐标为(﹣4,﹣![]() );
);
当△PBA∽△ABC时,∠CBA=∠PBA,
∴tan∠CBA=tan∠PBA,即![]() =
=![]() ,
,
∴![]() =
=![]() ,即n=﹣3a(m﹣1),
,即n=﹣3a(m﹣1),
∴![]() ,
,
解得,m1=﹣6,m2=1(不合题意,舍去),
当m=﹣6时,n=21a,
∵△PBA∽△ABC,
∴![]() =
=![]() ,即AB2=BCPB,
,即AB2=BCPB,
∴42=![]()
![]() ,
,
解得,a1=![]() (不合题意,舍去),a2=﹣
(不合题意,舍去),a2=﹣![]() ,
,
则点P的坐标为(﹣6,﹣![]() ),
),
综上所述,符合条件的点P的坐标为(﹣4,﹣![]() )和(﹣6,﹣
)和(﹣6,﹣![]() );
);
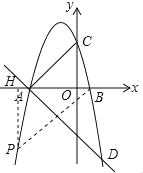
(3)作DM∥x轴交抛物线于M,作DN⊥x轴于N,作EF⊥DM于F,
则tan∠DAN=![]() =
=![]() =
=
∴∠DAN=60°,
∴∠EDF=60°,
∴DE=![]() =
=![]() EF,
EF,
∴Q的运动时间t=![]() +
+![]() =BE+EF,
=BE+EF,
∴当BE和EF共线时,t最小,
则BE⊥DM,E(1,﹣4![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家发明了一个魔术盒,当任意“数对”(a,b)进入其中时,会得到一个新的数:a2﹣b+1,例如把(3,﹣2)放入其中,就会得到32﹣(﹣2)+1=12,现将“数对”(﹣3,﹣2)放入其中后,得到的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个角是70°,则它的一个底角的度数是( )
A. 70° B. 70°或55° C. 80° D. 55°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(x,﹣4)与点N(2,y)关于y轴对称,则x﹣y的值为( )
A. ﹣6 B. 6 C. 2 D. ﹣2
-
科目: 来源: 题型:
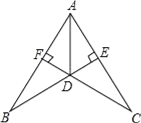
查看答案和解析>>【题目】如图,BE⊥AC、CF⊥AB于点E、F,BE与CF交于点D,DE=DF,连接AD.
求证:(1)∠FAD=∠EAD;
(2)BD=CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+
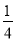 与y轴相交于点A,点B与点O关于点A对称
与y轴相交于点A,点B与点O关于点A对称(1)填空:点B的坐标是 ;
(2)过点B的直线y=kx+b(其中k<0)与x轴相交于点C,过点C作直线l平行于y轴,P是直线l上一点,且PB=PC,求线段PB的长(用含k的式子表示),并判断点P是否在抛物线上,说明理由;
(3)在(2)的条件下,若点C关于直线BP的对称点C′恰好落在该抛物线的对称轴上,求此时点P的坐标.
相关试题

