【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一点,
上一点,![]() 于点
于点![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为
为![]() 中点,
中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,
,![]() ≌
≌![]() .
.
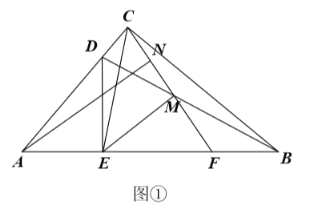
(1)求证:![]() ;
;
(2)求![]() 的大小;
的大小;
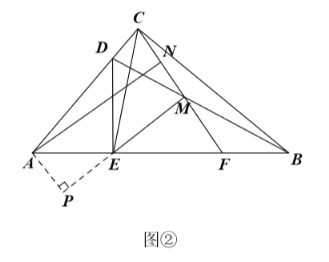
(3)如图②,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,求证:四边形
,求证:四边形![]() 为矩形.
为矩形.
参考答案:
【答案】(1)证明见解析;(2)∠MEF=30°;(3)证明见解析.
【解析】
(1)利用直角三角形斜边中线的性质定理可得CM=![]() DB,EM=
DB,EM=![]() DB,问题得证;
DB,问题得证;
(2)利用全等三角形的性质,证明△DEM是等边三角形,即可解决问题;
(3)设FM=a,则AE=CM=EM=![]() a,EF=2a,推出
a,EF=2a,推出![]() ,
,![]() ,得到AN∥PM,易证四边形ANMP是平行四边形,结合∠P=90°即可解决问题.
,得到AN∥PM,易证四边形ANMP是平行四边形,结合∠P=90°即可解决问题.
解:(1)证明:如图①中,
∵DE⊥AB,
∴∠DEB=∠DCB=90°,
∵DM=MB,
∴CM=![]() DB,EM=
DB,EM=![]() DB,
DB,
∴CM=EM;
(2)解:∵△DAE≌△CEM,CM=EM,
∴AE=ED=EM=CM=DM,∠AED=∠CME=90°
∴△ADE是等腰直角三角形,△DEM是等边三角形,
∵∠AED=∠DEF=90°,∠DEM=60°,
∴∠MEF=30°;
(3)证明:如图②中,设FM=a.
由(2)可知△ADE是等腰直角三角形,△DEM是等边三角形,∠MEF=30°,
∴AE=CM=EM=![]() a,EF=2a,
a,EF=2a,
∵CN=NM,
∴MN=![]() a,
a,
∴![]() ,
,![]() ,
,
∴EM∥AN,
∵AP⊥PM,MN⊥PM,
∴AP∥MN,
∴四边形ANMP是平行四边形,
∵∠P=90°,
∴四边形ANMP是矩形.
-
科目: 来源: 题型:
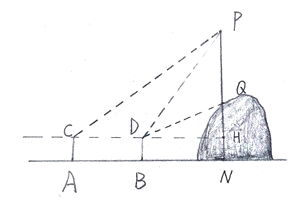
查看答案和解析>>【题目】小明学校门前有座山,山上有一电线杆PQ,他很想知道电线杆PQ 的高度.于是,有一天,小明和他的同学小亮带着侧倾器和皮尺来到山脚下进行测量.测量方案如下:如图,首先,小明站在地面上的点A处,测得电线杆顶端点P的仰角是45
 ;然后小明向前走6米到达点B处,测得电线杆顶端点P和电线杆底端点Q的仰角分别是60
;然后小明向前走6米到达点B处,测得电线杆顶端点P和电线杆底端点Q的仰角分别是60 和30
和30 ,设小明的眼睛到地面的距离为1.6米.请根据以上测量的数据,计算电线杆PQ的高度(结果精确到1米)参考数据:
,设小明的眼睛到地面的距离为1.6米.请根据以上测量的数据,计算电线杆PQ的高度(结果精确到1米)参考数据: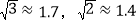 .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形
 的边长是1米;
的边长是1米;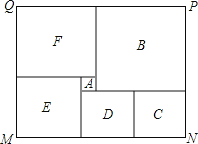
(1)若设图中最大正方形
 的边长是
的边长是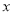 米,请用含
米,请用含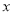 的代数式分别表示出正方形
的代数式分别表示出正方形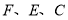 的边长
的边长(2)观察图形的特点可知,长方形相对的两边是相等的(即
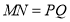 ,
, 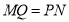 )请根据以上结论,求出
)请根据以上结论,求出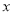 的值
的值(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
-
科目: 来源: 题型:
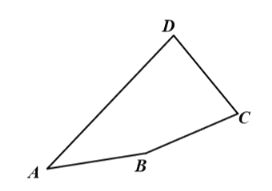
查看答案和解析>>【题目】如图,在凸四边形
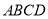 中,
中,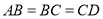 ,
,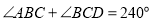 .
.
(1)利用尺规,以
 为边在四边形内部作等边
为边在四边形内部作等边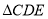 (保留作图痕迹,不需要写作法).
(保留作图痕迹,不需要写作法).(2)连接
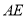 ,判断四边形
,判断四边形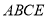 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】西安市阳光酸奶厂,每天生产A,B两种酸奶共800箱.A、B两种酸奶的成本和利润如下表.设每天生产A种酸奶x箱,两种酸奶共获利y元.

(1)请写出y关于x的函数关系式
(2)如果该酸奶厂每天至少投入成本48000元,那么每天最多获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若线段
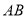 上有一点
上有一点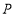 ,当
,当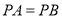 时,则称点
时,则称点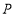 为线段
为线段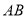 的中点.已知数轴上
的中点.已知数轴上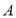 ,
,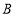 两点对应数分别为
两点对应数分别为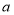 和
和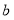 ,
,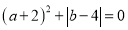 ,
,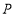 为数轴上一动点,对应数为
为数轴上一动点,对应数为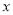 .
.(1)若点
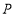 为线段
为线段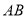 的中点,则
的中点,则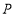 点对应的数
点对应的数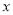 为______.若
为______.若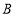 为线段
为线段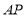 的中点时则
的中点时则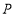 点对应的数
点对应的数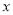 为______.
为______.(2)若点
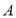 、点
、点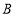 同时向左运动,它们的速度都为1个单位长度/秒,与此同时点
同时向左运动,它们的速度都为1个单位长度/秒,与此同时点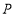 从-16处以2个单位长度/秒向右运动.
从-16处以2个单位长度/秒向右运动.①设运动的时间为
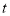 秒,直接用含
秒,直接用含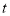 的式子填空
的式子填空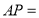 ______;
______;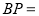 ______.
______.②经过多长时间后,点
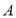 、点
、点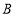 、点
、点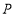 三点中其中一点是另外两点的中点?
三点中其中一点是另外两点的中点? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )
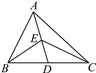
A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
相关试题

