【题目】定义:若线段![]() 上有一点
上有一点![]() ,当
,当![]() 时,则称点
时,则称点![]() 为线段
为线段![]() 的中点.已知数轴上
的中点.已知数轴上![]() ,
,![]() 两点对应数分别为
两点对应数分别为![]() 和
和![]() ,
,![]() ,
,![]() 为数轴上一动点,对应数为
为数轴上一动点,对应数为![]() .
.
(1)若点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点对应的数
点对应的数![]() 为______.若
为______.若![]() 为线段
为线段![]() 的中点时则
的中点时则![]() 点对应的数
点对应的数![]() 为______.
为______.
(2)若点![]() 、点
、点![]() 同时向左运动,它们的速度都为1个单位长度/秒,与此同时点
同时向左运动,它们的速度都为1个单位长度/秒,与此同时点![]() 从-16处以2个单位长度/秒向右运动.
从-16处以2个单位长度/秒向右运动.
①设运动的时间为![]() 秒,直接用含
秒,直接用含![]() 的式子填空
的式子填空
![]() ______;
______;![]() ______.
______.
②经过多长时间后,点![]() 、点
、点![]() 、点
、点![]() 三点中其中一点是另外两点的中点?
三点中其中一点是另外两点的中点?
参考答案:
【答案】(1)1 ,10;(2)①![]() 或
或![]() (或者写
(或者写![]() ),
),![]() 或
或![]() (或者写
(或者写![]() ),②
),②![]() 或
或![]() 或
或![]()
【解析】
(1)根据线段中点的定义得出规律,再利用规律解答即可.
(2)①根据题意得出A、B、P表示的数,从而得出结论;
②分三种情况讨论:若P为AB的中点,若A为BP的中点,若B为AP的中点,根据(1)所得结论列方程求解即可.
(1)∵P为线段AB的中点,∴AP=PB,
∴x-a=b-x,2x=a+b,
∴x=![]() ;
;
若B为线段AP的中点,则2b=a+x,解得:x=2b-a=8-(-2)=10.
故答案为:1,10.
(2)由题意得:A表示的数为-2-t,B表示的数为:4-t,P表示的数为:-16+2t.
①AP=|(-16+2t)-(-2-t)=|14-3t|,BP=|(-16+2t)-(4-t)|=|20-3t|,∴AP=-3t+14或14-3t;
BP=20-3t或3t-20.
故答案为:-3t+14或14-3t;20-3t或3t-20.
②分三种情况讨论:
若P为AB的中点,则:2(-16+2t)=(-2-t)+(4-t),解得:t=![]() ;
;
若A为BP的中点,则:2(-2-t)=(-16+2t)+(4-t),解得:t=![]() ;
;
若B为AP的中点,则:2(4-t)=(-2-t)+(-16+2t),解得:t=![]() .
.
-
科目: 来源: 题型:
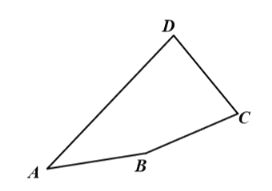
查看答案和解析>>【题目】如图,在凸四边形
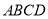 中,
中,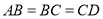 ,
,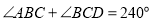 .
.
(1)利用尺规,以
 为边在四边形内部作等边
为边在四边形内部作等边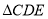 (保留作图痕迹,不需要写作法).
(保留作图痕迹,不需要写作法).(2)连接
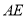 ,判断四边形
,判断四边形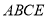 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,
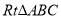 中,
中,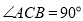 ,点
,点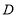 为边
为边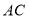 上一点,
上一点,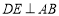 于点
于点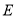 ,点
,点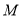 为
为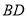 中点,点
中点,点 为
为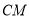 中点,
中点,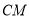 的延长线交
的延长线交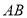 于点
于点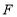 ,
,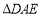 ≌
≌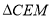 .
.
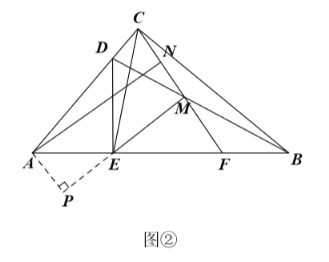
(1)求证:
 ;
;(2)求
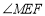 的大小;
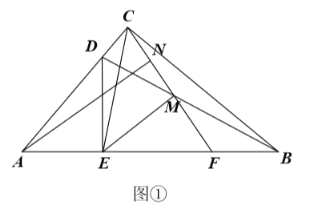
的大小;(3)如图②,过点
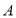 作
作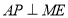 交
交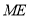 的延长线于点
的延长线于点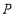 ,求证:四边形
,求证:四边形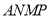 为矩形.
为矩形. -
科目: 来源: 题型:
查看答案和解析>>【题目】西安市阳光酸奶厂,每天生产A,B两种酸奶共800箱.A、B两种酸奶的成本和利润如下表.设每天生产A种酸奶x箱,两种酸奶共获利y元.

(1)请写出y关于x的函数关系式
(2)如果该酸奶厂每天至少投入成本48000元,那么每天最多获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )
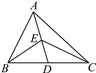
A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图有一张简易的活动小餐桌,现测得OA=OB=30cm,OC=OD=50cm,桌面离地面的高度为40cm,则两条桌腿的张角∠COD的度数为______度.
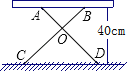
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
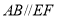 ,
,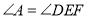 .在下列解答中,填空(理由或数学式):
.在下列解答中,填空(理由或数学式):
解:∵
 (已知),
(已知),∴
 (______),
(______),∵
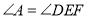 (已知),
(已知),∴∠______=∠______(等量代换),
∴
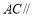 ______(______),
______(______),∴
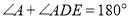 (______).
(______).
相关试题

