【题目】根据题意解答
(1)探究:如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E,若AE=8,求四边形ABCD的面积. 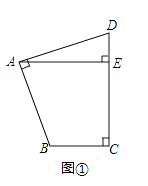
(2)应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=20,BC=10,CD=6,则四边形ABCD的面积为 . 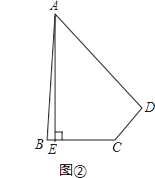
参考答案:
【答案】
(1)解:探究:如图1,过A作AF⊥BC,交CB的延长线于F,
∵AE⊥CD,∠C=90°
∴∠AED=∠F=∠C=90°,
∴四边形AFCE是矩形,
∴∠FAE=90°,
∵∠DAB=90°,
∴∠DAE=∠BAF=90°﹣∠BAE,
在△AFB和△AED中, 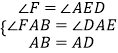 ,
,
∴△AFB≌△AED(AAS),
∴AE=AF=8,S△AFB=S△AED,
∵四边形AFCE是矩形,
∴四边形AFCE是正方形,
∴S正方形AFCE=8×8=64,
∴S四边形ABCD
=S四边形ABCE+S△AED
=S四边形ABCE+S△AFB
=S正方形AFCE
=64;
(2)160
【解析】(2)应用:如图2,过A作AF⊥CD,交CD的延长线于F, ∵AE⊥CD,
∴∠AED=∠F=90°,
∴∠FAE+∠BCD=180°,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠EAF,
∴∠BAD﹣∠EAD=∠EAF﹣∠EAD,
∴∠BAE=∠FAD,
在△AEB和△AFD中,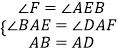 ,
,
∴△AEB≌△AFD(AAS),
∴AE=AF=19,BE=DF,
设BE=DF=x,
∵BC=10,CD=6,
∴CE=10﹣x,CF=6+x,
由勾股定理得;AC2=AE2+CE2=AF2+CF2 ,
∵AE=AF,
∴CE=CF,
即10﹣x=6+x,
解得:x=2,
∴CE=CF=8,
∵△AEB≌△AFD
∴S△AEB=S△AFD ,
∴S正方形AFCE= ![]() ×8×20+
×8×20+ ![]() ×8×20=160.
×8×20=160.
∴S四边形ABCD
=S△AEB+S四边形AECD
=S△AFD+S四边形AECD
=S正方形AFCE
=160.
所以答案是:160.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积是________.
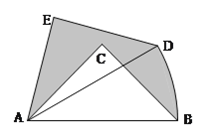
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b是一元二次方程x2﹣2x﹣1=0的两个实数根,则代数式(a﹣b)(a+b﹣2)+ab的值等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
⑴若ac=bc,则a=b;
⑵若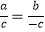 ,则a=﹣b;
,则a=﹣b;
⑶若x2=y2 , 则﹣4ax2=﹣4by2;
⑷若方程2x+5a=11﹣x与6x+3a=22的解相同,则a的值为0.
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
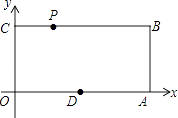
(1)△ODP的面积S= .
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题
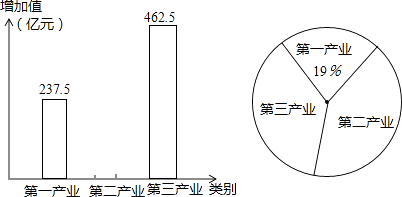
(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列数阵是由偶数排列而成的:
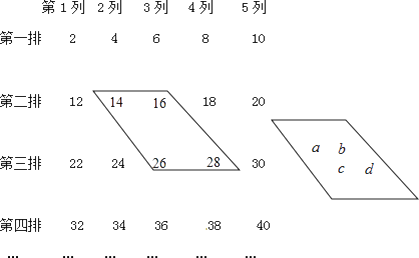
(1)在数阵中任意作一类似的框,如果这四个数的和为188,能否求出这四个数?如果能,求出这些数,如果不能,说明理由.如果和为288,能否求出这四个数?说明理由.
(2)有理数110在上面数阵中的第排、第列.
相关试题

