【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:![]() 微信、
微信、![]() 支付宝、
支付宝、![]() 现金、
现金、![]() 其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
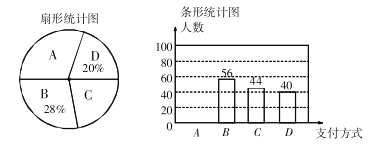
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中![]() 种支付方式所对应的圆心角为___________度;
种支付方式所对应的圆心角为___________度;
(3)若该超市这一周内有3200名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
参考答案:
【答案】(1)200(2)图见解析,108;(3)1856
【解析】
(1)根据D种支付方式的人数和所占百分比即可计算得出;
(2)根据总调查人数即可计算出A中支付方式的人数,再根据所占百分比即可计算出![]() 种支付方式所对应的圆心角度数;
种支付方式所对应的圆心角度数;
(3)根据总人数乘以A、B种支付方式所占百分比即可计算得出.
解:(1)40÷20%=200(名),
∴本次一共调查了200名购买者.
(2)200-56-44-40=60(名)
∴![]() 种支付方式的人数为60名,条形图如下图,
种支付方式的人数为60名,条形图如下图,
![]() ,
,
故![]() 种支付方式所对应的圆心角为108°,
种支付方式所对应的圆心角为108°,
故答案为:108.
(3)![]() (名)
(名)
答:使用A和B两种支付方式的购买者共有1856名.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。

(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
-
科目: 来源: 题型:
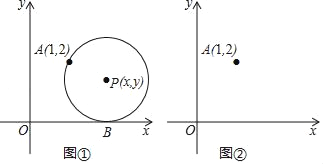
查看答案和解析>>【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,M、N分别是△ABC的边AC和AB的中点,D为BC上任意一点,连接AD,将△AMN沿AD方向平移到△A1M1N1的位置且M1N1在BC边上,已知△AMN的面积为7,则图中阴影部分的面积为( )
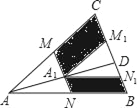
A. 14 B. 21 C. 28 D. 7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于_____.
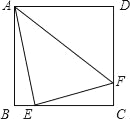
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为1厘米的6个相同正方体摆成如图的形式.

(1)该几何体的表面积为___________
 ;
;(2)如果在这个几何体上再添加一些相同的小正方体,使得从上面和从左面看到的图形保持不变,那么最多可以再添加__________个小正方体,并在下面的方格纸中画出添加小正方体后你从正面所看到的几何体形状图(画出符合条件中的一种即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.

(探究展示)
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
(拓展延伸)
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
相关试题

