【题目】已知直线l1:y=﹣2x+5和直线l2:y=x﹣4,直线l1与y轴交于点A,直线l2与y轴交于点B.

(1)求两条直线l1和l2的交点C的坐标;
(2)求两条直线与y轴围成的三角形的面积;
(3)已知点D是y轴上一点,若△BCD为等腰直角三角形,直接写出D点坐标.
参考答案:
【答案】(1)(3,﹣1);(2)![]() ;(3) (0,﹣1)或(0,2)
;(3) (0,﹣1)或(0,2)
【解析】
(1)解方程组即可得到两条直线l1和l2的交点C的坐标;
(2)根据点C为(3,﹣1),直线l1和l2与y轴的交点分别为A(0,5)、B(0,﹣4),即可得到两条直线与y轴围成的三角形的面积;
(3)分两种情况,根据函数图像及等腰直角三角形的特点即可求解.
解:(1)由题意得![]() ,
,
解方程组得![]()
∴l1和l2的交点C为(3,﹣1);
(2)如图,过点C作CE⊥y轴于E,则CE=3.
在y=﹣2x+5中,令x=0,则y=5,
在y=x﹣4中,令x=0,则y=﹣4,
∴直线l1和l2与y轴的交点分别为A(0,5)、B(0,﹣4),
则![]() =
=![]() =
=![]() =
=![]() ;
;
(3)分两种情况讨论:当∠BDC=90°时,点D与点E重合,即D(0,﹣1);
当∠BCD=90°时,BE=DE=3,DO=3﹣1=2,即D(0,2);
∴D点坐标为(0,﹣1)或(0,2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.

(1)求证:DC=BE;
(2)若∠AEC=69°,求∠EDG的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一次函数的表达式为y=
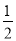 x﹣1
x﹣1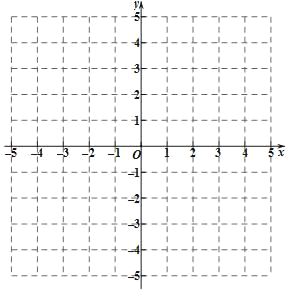
(1)该函数与x轴交点坐标为 ,与y轴的交点坐标为 ;
(2)画出该函数的图象(不必列表);
(3)根据该函数的图象回答下列问题:
①当x 时,则y>0;
②当﹣2≤x<4时,则y的取值范围是 .
-
科目: 来源: 题型:
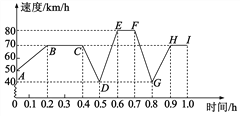
查看答案和解析>>【题目】汽车在山区行驶过程中,要经过上坡、下坡、平路等路段,在自身动力不变的情况下,上坡时速度越来越慢,下坡时速度越来越快乐,平路上保持匀速行驶,如图表示了一辆汽车在山区行驶过程中,速度随时间变化的情况.
(1)汽车在哪些时间段保持匀速行驶?时速分别是多少?
(2)汽车遇到了几个上坡路段?几个下坡路段?在哪个下坡路段上所花时间最长?
(3)用自己的语言大致描述这辆汽车的行驶情况,包括遇到的山路,在山路上的速度变化情况等.
-
科目: 来源: 题型:
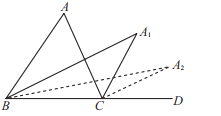
查看答案和解析>>【题目】如图,在
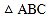 中,
中,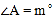 ,
,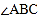 和
和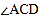 的平分线交于点
的平分线交于点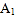 ,得
,得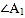 ;
;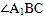 和
和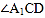 的平分线交于点
的平分线交于点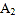 ,得
,得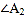 ;…;
;…;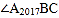 和
和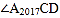 的平分线交于点
的平分线交于点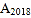 ,则
,则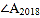 =___________.
=___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=
 x的图象的交点为C(m,4).
x的图象的交点为C(m,4).
(1)求一次函数y=kx+b的解析式;
(2)D是平面内一点,以O、C、D、B四点为顶点的四边形是平行四边形,直接写出点D的坐标.(不必写出推理过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图像可能是( )
A.
 B.
B. 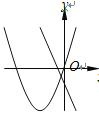 C.
C. 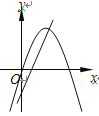 D.
D. 
相关试题

