【题目】如图,△ACB和△ECD中,∠ACB=∠ECD=a,且AC=BC,EC=DC,AE、BD交于P点,连CP
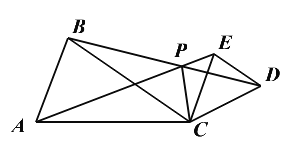
(1)求证:△ACE≌△BCD
(2)求∠APC的度数(用含a的式子表示)
参考答案:
【答案】(1)详见解析;(2)90°-![]() a.
a.
【解析】
(1)根据SAS即可证明结论;
(2)过C点分别作CH⊥AE,CG⊥BD,先利用全等的性质及三角形内角和证明∠BPA=∠ACB=a,再通过面积相等证明CH=CG,从而得到PC平分∠APD,然后利用角之间的关系即可得到结果.
解:(1)证明:∵∠ACB=∠DCE=a,
∴∠ACB+∠BCE=∠DCE+∠BCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中,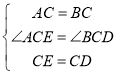 ,
,
∴△ACE≌△BCD(SAS);
(2)过C点分别作CH⊥AE于点H,CG⊥BD于点G,
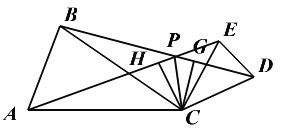
∵△ACE≌△BCD,
∴∠DBC=∠EAC,BD=AE,![]() ,
,
又∵∠BHP=∠AHC,
∴∠BPA=∠ACB=a,
∵![]() ,AE=BD,
,AE=BD,
∴CH=CG,
又∵CH⊥AE,CG⊥BD,
∴PC平分∠APD,
∴∠APC=![]() ∠APD=
∠APD=![]() (180°-∠BPA )=90°-
(180°-∠BPA )=90°-![]() a.
a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三年级261位学生参加期末考试,某班35位学生的语文成绩、数学成绩与总成绩在全年级中排名情况如图1和图2所示,甲、乙、丙为该班三位学生.

从这次考试成绩看,①在甲、乙两人中,总成绩名次靠前的学生是______;
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是______.
你选择的理由是____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七(1)班同学为了解2017年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理.请解答以下问题:
月均用水量

频数(户数)
百分比

6


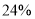

16


10


4

2


(1)请将下列频数分布表和频数分布直方图补充完整;
(2)求该小区月均用水量不超过
 的家庭占被调查家庭总数的百分比;
的家庭占被调查家庭总数的百分比;(3)若该小区有1000户家庭,根据调查数据估计该小区月均用水量超过
 的家庭数.
的家庭数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为( )
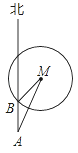
A. (
 ﹣1)小时 B. (
﹣1)小时 B. (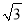 +1)小时 C. 2小时 D.
+1)小时 C. 2小时 D. 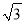 小时
小时 -
科目: 来源: 题型:
查看答案和解析>>【题目】“阳光”游泳馆为促进全民健身,2016年开始推行会员卡制度,标准如下表:
会员卡
办卡费用(元)
每次游泳收费(元)

50
25

200
20
(1)“阳光”游泳馆2016年5月销售
 ,
, 会员卡共104张,售卡收入14200元,请问这家游泳馆月销售
会员卡共104张,售卡收入14200元,请问这家游泳馆月销售 ,
, 会员卡各多少张?
会员卡各多少张?(2)小丽准备在“阳光”游泳馆购买会员卡,请你根据小丽游泳的次数,说明选择哪种会员卡最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读下面的材料并把解答过程补充完整.
问题:在关于
 ,
,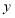 的二元一次方程组
的二元一次方程组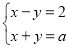 中,
中, ,
, ,求
,求 的取值范围.
的取值范围.在关于
 ,
,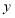 的二元一次方程组中,利用参数
的二元一次方程组中,利用参数 的代数式表示
的代数式表示 ,
,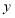 ,然后根据
,然后根据 ,
, 列出关于参数
列出关于参数 的不等式组即可求得
的不等式组即可求得 的取值范围.解:由
的取值范围.解:由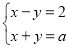 ,解得
,解得 ,又因为
,又因为 ,
, ,所以
,所以 解得____________.
解得____________.(2)请你按照上述方法,完成下列问题:
①已知
 ,且
,且 ,
, ,求
,求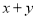 的取值范围;
的取值范围;②已知
 ,在关于
,在关于 ,
,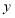 的二元一次方程组
的二元一次方程组 中,
中, ,
, ,请直接写出
,请直接写出 的取值范围(结果用含
的取值范围(结果用含 的式子表示)____________.
的式子表示)____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形纸片ABCD中,EF∥AB,M,N是线段EF的两个动点,且MN=
 EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
EF,若把该正方形纸片卷成一个圆柱,使点A与点B重合,若底面圆的直径为6cm,则正方形纸片上M,N两点间的距离是____________cm.
相关试题

