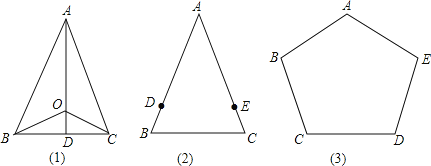
【题目】(1)如图(1),在△ABC,AB=AC,O为△ABC内一点,且OB=OC,求证:直线AO垂直平分BC.以下是小明的证题思路,请补全框图中的分析过程.

(2)如图(2),在△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.请你只用无刻度的直尺画出BC边的垂直平分线(不写画法,保留画图痕迹).
(3)如图(3),在五边形ABCDE中,AB=AE,BC=DE,∠B=∠E,请你只用无刻度的直尺画出CD边的垂直平分线,并说明理由.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
试题分析:(1)根据线段垂直平分线的性质定理的逆定理,只要AB=AC,OB=OC即可说明直线AO垂直平分BC;
(2)连结BE、CD相交于点O,则直线AO为BC边的垂直平分线;
(3)连结BD、CE相交于点O,则直线AO为CD边的垂直平分线.先证明ABC≌△AED得到AC=AD,∠ACB=∠ADE,根据等腰三角形的性质得∠ACD=∠ADC,所以∠BCD=∠EDC,再证明△BCD≌△ECD,则∠BDC=∠ECD,所以OD=OC,于是根据线段垂直平分线定理的逆定理即可判断直线AO为CD边的垂直平分线.
解:(1)

(2)如图(2),AO为所作;
(3)如图(3),AO为所作.
在△ABC和△AED中
 ,
,
∴△ABC≌△AED,
∴AC=AD,∠ACB=∠ADE,
∴∠ACD=∠ADC,
∴∠BCD=∠EDC,
在△BCD和△EDC中,
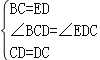 ,
,
∴△BCD≌△ECD,
∴∠BDC=∠ECD,
∴OD=OC,
∴AO垂直平分CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC边长为2,动点P从点A出发,以每秒1个单位长度的速度,沿A→B→C→A的方向运动,到达点A时停止.设运动时间为x秒,y=PC,则y关于x函数的图象大致为( )

A.
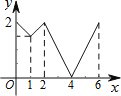 B.
B.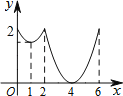
C.
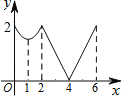 D.
D.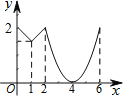
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
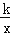 与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )
与y=﹣kx2+k(k≠0)在同一直角坐标系中的图象可能是( )A.
 B.
B.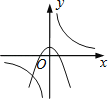 C.
C.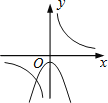 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣b=2,则代数式2a﹣2b﹣3的值是( )
A.1 B.2 C.5 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F分别是平行四边形ABCD的边AB,DC上的点,AF与DE相交于点P,FB与EC相交于点B,若S△APD=15cm2,S△BQC=25cm2,则阴影部分的面积为( )
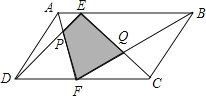
A.10cm2 B.20cm2 C.30cm2 D.40cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:函数y=
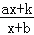 (a、b、k是常数,k≠ab)叫奇特函数.当a=b=0时,奇特函数y=
(a、b、k是常数,k≠ab)叫奇特函数.当a=b=0时,奇特函数y=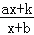 就是反比例函数y=
就是反比例函数y=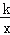 (k是常数,k≠0).
(k是常数,k≠0).(1)如果某一矩形两边长分别是2和3,当它们分别增加x和y后,得到新矩形的面积为8.求y与x之间的函数表达式,并判断它是否为奇特函数;
(2)如图,在平面直角坐标系xOy中,矩形OABC的顶点A、C坐标分别为(6,0)、(0,3),点D是OA中点,连接OB、CD交于E,若奇特函数y=
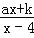 的图象经过点B、E,求该奇特函数的表达式;
的图象经过点B、E,求该奇特函数的表达式;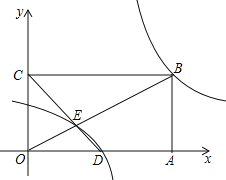
(3)把反比例函数y=
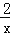 的图象向右平移4个单位,再向上平移 个单位就可得到(2)中得到的奇特函数的图象;
的图象向右平移4个单位,再向上平移 个单位就可得到(2)中得到的奇特函数的图象;(4)在(2)的条件下,过线段BE中点M的一条直线l与这个奇特函数图象交于P,Q两点(P在Q右侧),如果以B、E、P、Q为顶点组成的四边形面积为16,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中正确的个数为______.
(1)延长射线OA到点B;
(2)直线AB比射线CD长;
(3)线段AB就是A、B两点间的距离;
(4)角的大小与角两边的长度无关.
相关试题

