【题目】解方程与不等式组
(1)解方程: ![]() ;
;
(2)解不等式组:  .
.
参考答案:
【答案】
(1)解:方程两边都乘x(x+3),得
2(x+3)=3x,
解得x=6.
检验:当x=6时,x(x+3)≠0.
∴x=6是原方程的解.
(2)解:解不等式①,得x>3,
解不等式②,得x≤10.
∴这个不等式组的解集为3<x≤10.
【解析】(1)本题的最简公分母是x(x+3),方程两边都乘最简公分母,可把分式方程转换为整式方程求解.结果要检验.(2)首先求出每个不等式的解集,再运用口诀:“大小小大中间找”求出这些不等式解集的公共部分.
【考点精析】本题主要考查了去分母法和一元一次不等式组的解法的相关知识点,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y=
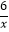 与边AB、BC分别交于D、E两点,OE交双曲线y=
与边AB、BC分别交于D、E两点,OE交双曲线y= 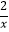 于点G,若DG∥OA,OA=3,则CE的长为( )
于点G,若DG∥OA,OA=3,则CE的长为( ) 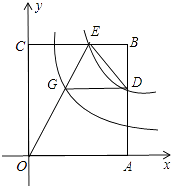
A.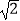
B.1.5
C.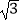
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,那么∠B= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2 , 则四边形PFCG的面积为cm2 .
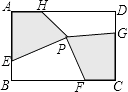
-
科目: 来源: 题型:
查看答案和解析>>【题目】一不透明的袋子中装有4个球,它们除了上面分别标有的号码1、2、3、4不同外,其余均相同.将小球搅匀,并从袋中任意取出一球后放回;再将小球搅匀,并从袋中再任意取出一球.若把两次号码之和作为一个两位数的十位上的数字,两次号码之差的绝对值作为这个两位数的个位上的数字,请用“画树状图”或“列表”的方法求所组成的两位数是奇数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
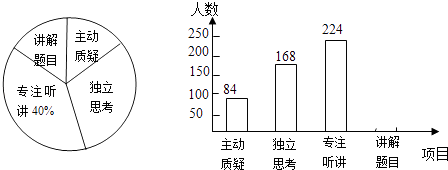
(1)在这次评价中,一共抽查了名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,O是BC上一点,以点O为圆心,OB长为半径作圆,恰好经过点A,并与BC交于点D.

(1)判断直线CA与⊙O的位置关系,并说明理由;
(2)若AB= ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).
相关试题

