【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠EDF的度数为( )

A.34°B.56°C.62°D.28°
参考答案:
【答案】A
【解析】
先利用互余计算出∠FDB=28°,再根据平行线的性质得∠CBD=∠FDB=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DFE的度数,于是得到结论.
解:∵四边形ABCD为矩形,
∴AD∥BC,∠ADC=90°,
∵∠BDC=62°,
∴∠FDB=90°﹣∠BDC=90°﹣62°=28°,
∵AD∥BC,
∴∠CBD=∠FDB=28°,
∵矩形ABCD沿对角线BD折叠,
∴∠FBD=∠CBD=28°,
∴∠DFE=∠FBD+∠FDB=28°+28°=56°.
∴∠EDF=90°﹣∠EFD=90°﹣56°=34°,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
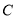 点是第二象限内一点,
点是第二象限内一点, 轴于
轴于 ,且
,且 是
是 轴正半轴上一点,
轴正半轴上一点, 是x轴负半
是x轴负半 轴上一点,且
轴上一点,且 .
.
(1)
 ( ),
( ), ( )
( )(2)如图2,设
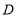 为线段
为线段 上一动点,当
上一动点,当 时,
时, 的角平分线与
的角平分线与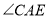 的角平分线的反向延长线交于点
的角平分线的反向延长线交于点 ,求
,求 的度数: (注: 三角形三个内角的和为
的度数: (注: 三角形三个内角的和为 )
) (3)如图3,当
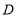 点在线段
点在线段 上运动时,作
上运动时,作 交
交 于
于 的平分线交于
的平分线交于 ,当
,当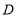 点在运动的过程中,
点在运动的过程中, 的大小是否变化?若不变,求出其值;若变化,请说明理由.
的大小是否变化?若不变,求出其值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=
 ,BE=2.
,BE=2.
求证:(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,在某个时刻停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶纪录如下(单位:千米)
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
. (1)
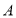 在岗亭哪个方向?距岗亭多远?
在岗亭哪个方向?距岗亭多远? (2)若摩托车行驶每千米耗油
 升,每升
升,每升 元,且最后返回岗亭,这一天耗油共需多少元?
元,且最后返回岗亭,这一天耗油共需多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点
 表示的数为
表示的数为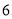 ,点
,点 表示的数为
表示的数为 ,点
,点 到点
到点 、点
、点 的距离相等,动点
的距离相等,动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿数轴向右匀速运动,设运动时间为
个单位长度的速度沿数轴向右匀速运动,设运动时间为 (
( 大于
大于 秒.
秒.
(1)点
 表示的数是______.
表示的数是______.(2)求当
 等于多少秒时,点
等于多少秒时,点 到达点
到达点 处?
处?(3)点
 表示的数是______(用含字母
表示的数是______(用含字母 的式子表示)
的式子表示)(4)求当
 等于多少秒时,
等于多少秒时, 、
、 之间的距离为
之间的距离为 个单位长度.
个单位长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】一种竹制躺椅如图①所示,其侧面示意图如图②③所示,这种躺椅可以通过改变支撑杆CD的位置来调节躺椅舒适度.假设AB所在的直线为地面,已知AE=120 cm,当把图②中的支撑杆CD调节至图③中的C′D的位置时,∠EAB由20°变为25°.
(1)你能求出调节后该躺椅的枕部E到地面的高度增加了多少吗?(结果精确到0.1 cm,参考数据:sin 20°≈0.342 0,sin 25°≈0.422 6)
(2)已知点O为AE的一个三等分点,根据人体工程学,当点O到地面的距离为26 cm时,人体感觉最舒适.请你求出此时枕部E到地面的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,∠ABE=
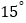 ,且AB=AE,则DE的长度为( )
,且AB=AE,则DE的长度为( )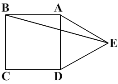
A. 3 B. 4 C. 5 D. 6
相关试题

