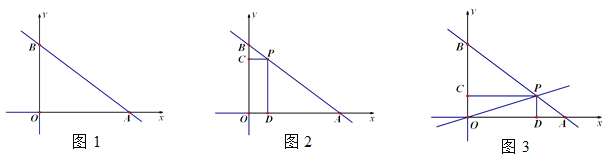
【题目】如图,在平面直角坐标系中,直线![]() 分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D.设点P的横坐标为m.
分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D.设点P的横坐标为m.
(1)如图1,求线段AB的长度;
(2)如图2,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)如图3,作直线OP,若直线OP的解析式为![]() ,求四边形OCPD的周长.
,求四边形OCPD的周长.
参考答案:
【答案】(1)5;(2)P(1,![]() )(3)
)(3)![]()
【解析】
(1)根据解析式求出A,B的坐标即可求出AB的长度;
(2)先求出CP的长为1,故P点横坐标为1,代入解析式求出P点坐标;
(3)联立两函数求出P的坐标,即可求出四边形OCPD的周长.
(1)令x=0,得y=3,∴B(0,3)
令y=0.解得x=4,∴A(4,0)
∴AB=![]()
(2) ![]() =1,
=1,
把x=1代入![]()
得y=![]()
∴P(1,![]() )
)
(3)联立两函数,即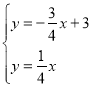 解得
解得![]()
∴P(3,![]() )
)
∴四边形OCPD的周长为![]()
-
科目: 来源: 题型:
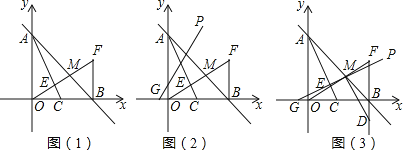
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,直线y=-x+m交y轴于点A,交x轴于点B,点C为OB的中点,作C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
(1)直接写出点F的坐标(用m表示);
(2)求证:OF⊥AC;
(3)如图(2),若m=2,点G的坐标为(-
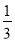 ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;①求k的取值范围;
②如图(3),若直线GP经过点M,过点M作GM的垂线交FB的延长线于点D,在平面内是否存在点Q,使四边形DMGQ为正方形?如果存在,请求出Q点坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。

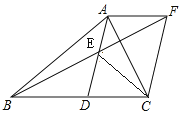
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行1500米比赛,在比赛时,两人所跑的路程y(米)与所用的时间x(分)间的函数关系如图所示,解答下列问题:
(1)求甲的速度等于多少米/分;
(2)当乙到终点时,甲距离终点有多远;
(3)乙在距终点多远处追上了甲.
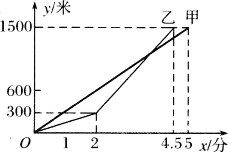
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;
(2)以O点为位似中心,将△AEF作位似变换且缩小为原来的
 ,在网格内画出一个符合条件的△A1E1F1.
,在网格内画出一个符合条件的△A1E1F1.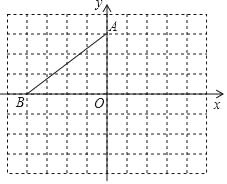
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:将连续的偶2,4,6,8,…,排成如表:
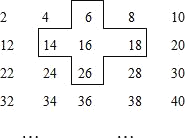
(1)请你求出十字框中的五个数的和;
(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
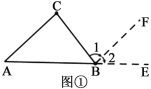
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
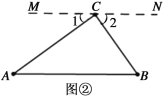
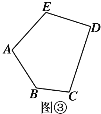
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
相关试题

