【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。

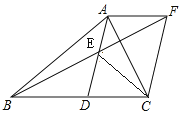
图1 图2
参考答案:
【答案】(1)见解析(2) △CFE、 △ABD、 △ACD 、△ACF、 △ABF
【解析】试题分析:(1)先证明△AEF≌△DEB,得到AF=DB,又由BD=CD,得到AF=CD.
由一组对边平行且相等的四边形是平行四边形即可得到结论.
(2)与△BEC面积相等的三角形有△CFE、 △ABD、 △ACD 、△ACF、 △ABF.
试题解析:(1)证明:∵D为BC的点、E为AD的中点,∴BD=CD,AE=DE.
∵AF∥BC,∴∠AFE=∠DBE.
在△AEF和△DEB中,∵∠AFE=∠DBE,∠AEF=∠DEB,AE=DE,∴ △AEF≌△DEB,
∴AF=DB.又∵BD=CD,∴AF=CD.
又∵AF∥BC,∴四边形ADCF是平行四边形.
(2)△CFE、 △ABD、 △ACD 、△ACF、 △ABF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,D为AB的中点,F为BC边上一点,连接CD、AF交干点E.若∠FAC=90°-3∠BAF,BF:AC=2:5,EF=2,则AB长为__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC,点C在小正方形的顶点上,且tan∠B=3;
(2)在图中画一个以AB为底的等腰三角形△ABD,点D在小正方形的项点上,且△ABD是锐角三角形.连接CD,请直接写出线段CD的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着2018年两会的隆重召开,中学校园掀起了关注时事政治的热潮我区及时开展“做一个关心国家大事的中学生”主题活动。为了了解我区中学生获取时事新闻的主要途径,分别从电脑上网、手机上网、听广播、看电视、看报纸五个方面,在全区范围内随机抽取了若干名中学生进行问卷调查(每名中学生只选一种主要途径),根据调查结果绘制了如图所示的不完整的统计图请根据统计图的信息回答下列问题:

(1)本次调查共抽取了中学生多少人?
(2)求本次调查中,以听广播获取时事新闻为主要途径的人数并补全条形统计图;
(3)若本区共有中学生7000人,请你估计我区以看电视以看电视获取时事新闻为主要途径的中学生有多少人?
-
科目: 来源: 题型:
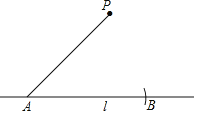
查看答案和解析>>【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点P作已知直线l的平行线”.
小明的作法如下:
①在直线l上取一点A,以点A为圆心,AP长为半径作弧,交直线l于点B;
②分别以P,B为圆心,以AP长为半径作弧,两弧相交于点Q(与点A不重合);
③作直线PQ.所以直线PQ就是所求作的直线.根据小明的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=AP= = .
∴四边形ABQP是菱形( )(填推理的依据).
∴PQ∥l.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
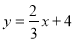 与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.
与x轴、y轴分别交于点A和点B,点C在线段AB上,点D在y轴的负半轴上,C、D两点到x轴的距离均为2.(1)点C的坐标为 ,点D的坐标为 ;
(2)点P为线段OA上的一动点,当PC+PD最小时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=12,P是线段AB的三等点,Q是直线AB上一个动点,若AQ=PQ+BQ,则线段AQ的长为__________________
相关试题

