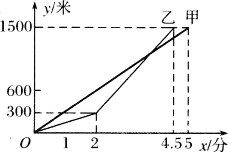
【题目】甲、乙两人进行1500米比赛,在比赛时,两人所跑的路程y(米)与所用的时间x(分)间的函数关系如图所示,解答下列问题:
(1)求甲的速度等于多少米/分;
(2)当乙到终点时,甲距离终点有多远;
(3)乙在距终点多远处追上了甲.
参考答案:
【答案】(1)300米/分;
(2)150m;
(3)400m
【解析】
(1)根据图像即可求解;
(2)利用待定系数法确定函数关系式分别求出甲乙的函数解析式即可求解;
(3)令两函数相等求出交点坐标,即可得到答案.
(1)甲的速度为![]() =300米/分;
=300米/分;
(2)甲的所跑的路程y(米)与所用的时间x(分)间的函数关系为y1=300x;
x=4.5时,y1=1350,
1500-1350=150m
∴当乙到终点时,甲距离终点有150m;
(2)
设乙在2≤x≤4.5时,函数解析式为y2=kx+b,
把(2,300)和(4.5,1500)代入得![]()
解得k=480,b=-660
∴2≤x≤4.5, y2=480x-660
令y1= y2,即300x=480x-660
解得x=3![]()
x=3![]() ,y1=1100,
,y1=1100,
1500-1100=400,
故乙在距终点400m追上甲.
-
科目: 来源: 题型:
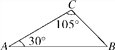
查看答案和解析>>【题目】如图,已知AC=4,求AB和BC的长.
-
科目: 来源: 题型:
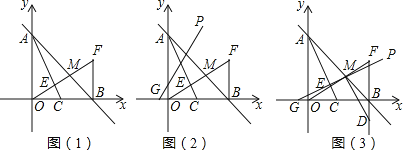
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,直线y=-x+m交y轴于点A,交x轴于点B,点C为OB的中点,作C关于直线AB的对称点F,连接BF和OF,OF交AC于点E,交AB于点M.
(1)直接写出点F的坐标(用m表示);
(2)求证:OF⊥AC;
(3)如图(2),若m=2,点G的坐标为(-
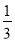 ,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;
,0),过G点的直线GP:y=kx+b(k≠0)与直线AB始终相交于第一象限;①求k的取值范围;
②如图(3),若直线GP经过点M,过点M作GM的垂线交FB的延长线于点D,在平面内是否存在点Q,使四边形DMGQ为正方形?如果存在,请求出Q点坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。

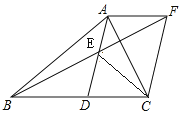
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
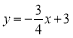 分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D.设点P的横坐标为m.
分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合),过点P分别作PC⊥y轴于点C,PD⊥x轴于点D.设点P的横坐标为m.(1)如图1,求线段AB的长度;
(2)如图2,当
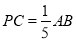 时,求点P的坐标;
时,求点P的坐标;(3)如图3,作直线OP,若直线OP的解析式为
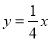 ,求四边形OCPD的周长.
,求四边形OCPD的周长.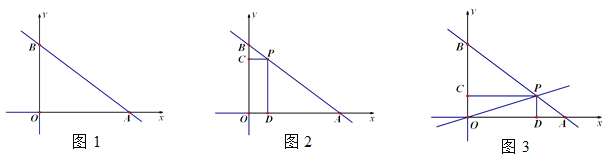
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),
(1)将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;
(2)以O点为位似中心,将△AEF作位似变换且缩小为原来的
 ,在网格内画出一个符合条件的△A1E1F1.
,在网格内画出一个符合条件的△A1E1F1.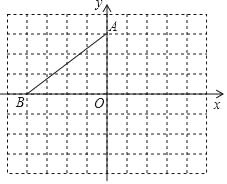
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:将连续的偶2,4,6,8,…,排成如表:
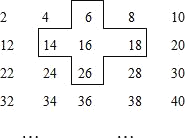
(1)请你求出十字框中的五个数的和;
(2)设中间的数为x,请你用含x的式子表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,这五个数的和能等于2018吗?如能,写出这五个数,如不能,请说明理由.
相关试题

