【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+ ![]() 与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,点D与点C关于抛物线的对称轴对称.
(1)求抛物线的解析式,并直接写出点D的坐标;
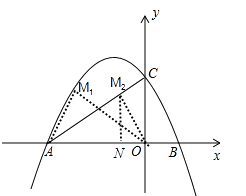
(2)如图1,点P从点A出发,以每秒1个单位长度的速度沿A→B匀速运动,到达点B时停止运动.以AP为边作等边△APQ(点Q在x轴上方).设点P在运动过程中,△APQ与四边形AOCD重叠部分的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式;
(3)如图2,连接AC,在第二象限内存在点M,使得以M、O、A为顶点的三角形与△AOC相似.请直接写出所有符合条件的点M坐标.
参考答案:
【答案】
(1)解:∵抛物线y=ax2+bx+ ![]() 经过A(﹣3,0),B(1,0)两点,
经过A(﹣3,0),B(1,0)两点,
∴ ![]() ,
,
解得 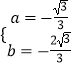 ,
,
∴抛物线解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ;
;
则D点坐标为(﹣2, ![]() )
)
(2)解:∵点D与A横坐标相差1,纵坐标之差为 ![]() ,则tan∠DAP=
,则tan∠DAP= ![]() ,
,
∴∠DAP=60°,
又∵△APQ为等边三角形,
∴点Q始终在直线AD上运动,当点Q与D重合时,由等边三角形的性质可知:AP=AD= ![]() .
.
①当0≤t≤2时,P在线段AO上,此时△APQ的面积即是△APQ与四边形AOCD的重叠面积.
AP=t,
∵∠QAP=60°,
∴点Q的纵坐标为tsin60°= ![]() t,
t,
∴S= ![]() ×
× ![]() t×t=
t×t= ![]() t2.
t2.
②当2<t≤3时,如图:
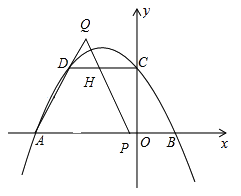
此时点Q在AD的延长线上,点P在OA上,
设QP与DC交于点H,
∵DC∥AP,
∴∠QDH=∠QAP=∠QHD=∠QPA=60°,
∴△QDH是等边三角形,
∴S=S△QAP﹣S△QDH,
∵QA=t,
∴S△QAP= ![]() t2.
t2.
∵QD=t﹣2,
∴S△QDH= ![]() (t﹣2)2,
(t﹣2)2,
∴S= ![]() t2﹣
t2﹣ ![]() (t﹣2)2=
(t﹣2)2= ![]() ﹣
﹣ ![]() .
.
③当3<t≤4时,如图:
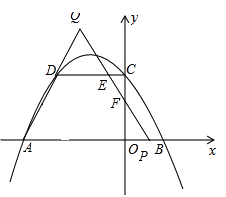
此时点Q在AD的延长线上,点P在线段OB上,
设QP与DC交于点E,与OC交于点F,过点Q作AP的垂涎,垂足为G,
∵OP=t﹣3,∠FPO=60°,
∴OF=OPtan60°= ![]() t﹣3),
t﹣3),
∴S△FOP= ![]() ×
× ![]() (t﹣3)(t﹣3)=
(t﹣3)(t﹣3)= ![]() (t﹣3)2,
(t﹣3)2,
∵S=S△QAP﹣S△QDE﹣S△FOP,S△QAP﹣S△QDE= ![]() t﹣
t﹣ ![]() .
.
∴S= ![]() t﹣
t﹣ ![]() ﹣
﹣ ![]() (t﹣3)2=
(t﹣3)2= ![]() t2+4
t2+4 ![]() t﹣
t﹣ ![]() .
.
综上所述,S与t之间的函数关系式为 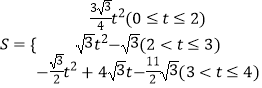
(3)解:∵OC= ![]() ,OA=3,OA⊥OC,则△OAC是含30°的直角三角形.
,OA=3,OA⊥OC,则△OAC是含30°的直角三角形.
①当△AMO以∠AMO为直角的直角三角形时;如图,过点M2作AO的垂线,垂足为N,
∵∠M2AO=30°,AO=3,
∴M2O= ![]() ,
,
又∵∠OM2N=M2AO=30°,
∴ON= ![]() OM2=
OM2= ![]() ,M2N=
,M2N= ![]() ON
ON ![]() ,
,
∴M2的坐标为(﹣ ![]() ,
, ![]() ).
).
同理可得M1的坐标为(﹣ ![]() ,
, ![]() ).
).
②当△AMO以∠OAM为直角的直角三角形时;如图:
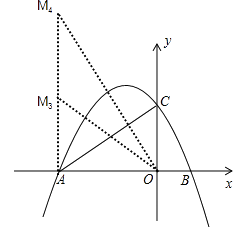
∵以M、O、A为顶点的三角形与△OAC相似,
∴ ![]() ,或
,或 ![]() =
= ![]() ,
,
∵OA=3,
∴AM= ![]() 或AM=
或AM= ![]() ,
,
∵AM⊥OA,且点M在第二象限,
∴点M的坐标为(﹣3, ![]() )或(﹣3,3
)或(﹣3,3 ![]() ).
).
综上所述,符合条件的点M的所有可能的坐标为(﹣3, ![]() ),(﹣3,3
),(﹣3,3 ![]() ),(
),( ![]() ,
, ![]() ,(﹣
,(﹣ ![]() ,
, ![]() ).
).
【解析】(1)把A、B两点的坐标代入抛物线解析式,求出抛物线的解析式,由抛物线与y轴交于点C,点D与点C关于抛物线的对称轴对称,由顶点式得到D点坐标;(2)由点D与A横坐标相差1,纵坐标之差为 3 ,得到tan∠DAP= 3 ,∠DAP=60°,又△APQ为等边三角形,得到点Q始终在直线AD上运动,当点Q与D重合时,由等边三角形的性质和勾股定理求出:AP=AD的值;①当0≤t≤2时,P在线段AO上,此时△APQ的面积即是△APQ与四边形AOCD的重叠面积;②当2<t≤3时,此时点Q在AD的延长线上,点P在线段OB上,根据已知条件和三角形的面积公式,得到S与t之间的三种函数关系式;(3)根据已知可得△OAC是含30°的直角三角形,①当△AMO以∠AMO为直角的直角三角形时,根据在直角三角形中,30度角所对的边是斜边的一半,求出M2的坐标,同理可得M1的坐标;②当△AMO以∠OAM为直角的直角三角形时,以M、O、A为顶点的三角形与△OAC相似,得到比例,求出AM的值,得到点M的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:
 ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,锐角
 中,
中, ,若想找一点P,使得
,若想找一点P,使得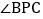 与
与 互补,甲、乙、丙三人作法分别如下:
互补,甲、乙、丙三人作法分别如下:甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求;
乙:分别以B,C为圆心,AB,AC长为半径画弧交于P点,则P即为所求;
丙:作BC的垂直平分线和
 的平分线,两线交于P点,则P即为所求.
的平分线,两线交于P点,则P即为所求.对于甲、乙、丙三人的作法,下列叙述正确的是



A. 三人皆正确B. 甲、丙正确,乙错误
C. 甲正确,乙、丙错误D. 甲错误,乙、丙正确
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以边AB为直径作⊙O,交BC于点D,过D作DE⊥AC于点E.
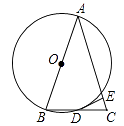
(1)求证:DE为⊙O的切线;
(2)若AB=13,sinB= ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 ,当
,当  时对应的函数图像位于
时对应的函数图像位于  轴的下方,当
轴的下方,当  时对应的函数图像位于
时对应的函数图像位于  轴的上方,则
轴的上方,则  的值为( )
的值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】玲玲家准备装修一套新住房,若甲、乙两个装饰公司合作,需6周完成,共需装修费为5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费4.8万元.玲玲的爸爸妈妈商量后决定只选一个公司单独完成.
(1)如果从节约时间的角度考虑应选哪家公司?
(2)如果从节约开支的角度考虑呢?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:
 记为
记为  ,它与
,它与  轴交于两点
轴交于两点  ,
,  ;将
;将  绕
绕  旋转
旋转  得到
得到  ,交
,交  轴于
轴于  ;将
;将  绕
绕  旋转
旋转  得到
得到  ,交
,交  轴于
轴于  ;…如此进行下去,直至得到
;…如此进行下去,直至得到  ,若点
,若点  在第
在第  段抛物线
段抛物线  上,则
上,则  .
. 
相关试题

