【题目】如图,在等腰Rt△ABC中,∠ABC=90°,AB=BC,D为斜边AC延长线上一点,过D点作BC的垂线交其延长线于点E,在AB的延长线上取一点F,使得BF=CE,连接EF.
(1)若AB=2,BF=3,求AD的长度;
(2)G为AC中点,连接GF,求证:∠AFG+∠BEF=∠GFE.

参考答案:
【答案】(1)5![]() (2)见详解
(2)见详解
【解析】
(1)易证DE∥AB,可得△ABC∽△DEC,即可证明△CDE为等腰直角三角形,根据CE即可求得CD的长,根据AB可求得AC的长,根据AD=AC+CD即可解题;
(2)连接EG、BG,易证BG=CG,∠ABG=∠ACB=45°,即可证明△GBF≌△GCE,可得GE=GF,∠BGF=∠CGE,∠AFG=∠BEG,即可证明△EFG为等腰直角三角形,可得∠GFE=∠GEF,根据∠GEF=∠BEG+∠BEF即可解题.
(1)∵DE⊥BE,AB⊥BE,
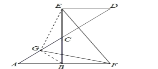
∴DE∥AB,
∴△ABC∽△DEC,
∴△CDE为等腰直角三角形,
∵CE=BF=3,∴CD=3![]() ,
,
∵AB=2,∴AC=2![]() ,
,
∴AD=AC+CD=5![]() ;
;
(2)连接EG、BG,证明△GBF≌△GCE.:∠AFG+∠BEF=∠GFE.
∵G是等腰直角△ABC斜边AC中点,
∴BG=CG,∠ABG=∠ACB=45°,
∴∠GBF=∠GCE=135°,
∵在△GBF和△GCE中, GB=GC,∠GBF=∠GCE,BF=CE,
∴△GBF≌△GCE,(SAS)
∴GE=GF,∠BGF=∠CGE,∠AFG=∠BEG,
∵∠BGF+∠FGC=90°,
∴∠CGE+∠FGC=90°,即∠EGF=90°,
∴△EFG为等腰直角三角形,
∴∠GFE=∠GEF=45°,
∵∠GEF=∠BEG+∠BEF,
∴∠GEF=∠AFG+∠BEF,
∴∠AFG+∠BEF=∠GFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=_____.

-
科目: 来源: 题型:
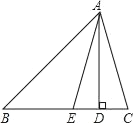
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线.
(1)若∠B=38°,∠C=70°,求∠DAE的度数;
(2)若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣  )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 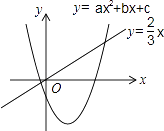
A.大于0
B.等于0
C.小于0
D.不能确定 -
科目: 来源: 题型:
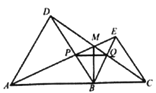
查看答案和解析>>【题目】如图,点A,B,C在同一直线上,在这条直线同侧作等边△ABD和等边△BCE,连接AE和CD,交点为M,AE交BD于点P,CD交BE于点Q,连接PQ、BM, 有4个结论:①△ABE≌△DBC,②△DQB≌△ABP,③∠EAC=30°,④∠AMC=120°,请将所有正确结论的序号填在横线上______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察以下等式:
第1个等式:
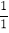 +
+ +
+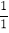 ×
× =1,
=1,第2个等式:
 +
+ +
+ ×
× =1,
=1,第3个等式:
 +
+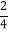 +
+ ×
×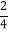 =1,
=1,第4个等式:
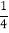 +
+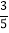 +
+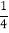 ×
×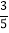 =1,
=1,第5个等式:
 +
+ +
+ ×
× =1,
=1,……
按照以上规律,解决下列问题:
(1)写出第6个等式:_____;
(2)写出你猜想的第n个等式:_____(用含n的等式表示),并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若我们规定三角“
 ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题:(1)计算:
 = ______ ;
= ______ ;(2)代数式
 为完全平方式,则k= ______ ;
为完全平方式,则k= ______ ;(3)解方程:
 =6x2+7.
=6x2+7.
相关试题

