Question

【题目】阅读下列材料：如图(1)，在四边形ABCD中，若AB=AD，BC=CD，则把这样的四边形称之为筝形．

(1)写出筝形的两个性质(定义除外)．

① ；② ．

(2)如图(2)，在平行四边形ABCD中，点E、F分别在BC、CD上，且AE=AF，∠AEC=∠AFC．求证：四边形AECF是筝形．

(3)如图(3)，在筝形ABCD中，AB=AD=26，BC=DC=25，AC=17，求筝形ABCD的面积．

Answer 1

【答案】（1）∠BAC＝∠DAC；∠ABC＝∠ADC（2）见解析（3）408

【解析】

（1）根据题意证明△ABC≌△ADC即可，

（2）先判断出∠AEB＝∠AFD在得到△AEB≌△AFD，然后判断出平行四边形ABCD是菱形即可；

（3）先判断出△ABC≌△ADC．得到S△ABC＝S△ADC，过点B作BH⊥AC，垂足为H，利用勾股定理BH2＝AB2AH2＝262AH2，BH2＝CB2CH2＝252（17AH）2，求出AH,BH即可求解．

（1）在△ABC和△ADC中，

，

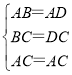∴△ABC≌△ADC

∴∠BAC＝∠DAC，∠ABC＝∠ADC，

故答案为：∠BAC＝∠DAC；∠ABC＝∠ADC

（2）证明：∵四边形ABCD是平行四边形，

∴∠B＝∠D．

∵∠AEC＝∠AFC，∠AEC＋∠AEB＝∠AFC＋∠AFD＝180°，

∴∠AEB＝∠AFD．

∵AE＝AF，

∴△AEB≌△AFD（AAS）．

∴AB＝AD，BE＝DF．

∴平行四边形ABCD是菱形．

∴BC＝DC，

∴EC＝FC，

∴四边形AECF是筝形．

（3）如图

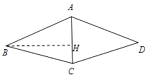
∵AB＝AD，BC＝DC，AC＝AC，

∴△ABC≌△ADC．

∴S△ABC＝S△ADC．

过点B作BH⊥AC，垂足为H．

在Rt△ABH中，BH2＝AB2AH2＝262AH2．

在Rt△CBH中，BH2＝CB2CH2＝252（17AH）2．

∴262AH2＝252（17AH）2，

∴AH＝10．

∴BH＝=24．

∴S△ABC＝×17×24＝204．

∴筝形ABCD的面积=2S△ABC＝408．