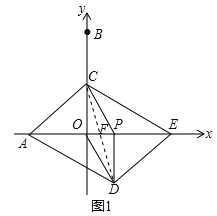
【题目】如图，在平面直角坐标系中，点A、B的坐标分别是（－2，0）、（0，4）.动点P从O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C以每秒2个单位的速度在y轴上从点B出发运动到点O停止，点C停止运动时点P也随之停止运动.以CP、CO为邻边构造□PCOD，在线段OP的延长线长取点E，使得PE=2.设点P的运动时间为t秒．

（1）求证:四边形ADEC是平行四边形；

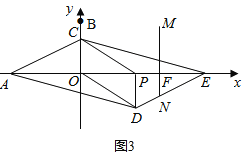
（2）以线段PE为对角线作正方形MPNE，点M、N分别在第一、四象限.

①当点M、N中有一点落在四边形ADEC的边上时，求出所有满足条件的t的值；

②若点M、N中恰好只有一点落在四边形ADEC的内部（不包括边界）时，设□PCOD的面积为S，直接写出S的取值范围.

参考答案：

【答案】（1）证明见解析；（2）t=或t=1；（3）≤S＜2．

【解析】

试题分析：（1）连接CD交OP于点G，由PCOD的对角线互相平分，得四边形ADEC是平行四边形；

（2）①第一种情况，当点M在CE边上时，由△EMF∽△ECO，再利用正方形对角线相等求解；第二种情况，当点N在DE边上时，由△EFN∽△EPD，再利用正方形对角线相等求解；

②当≤t≤1时，求出S的取值范围．

试题解析：（1）如图1，连接CD交AE于F，

∵四边形PCOD是平行四边形，

∴CF=DP，OF=PF，

∵PE=AO，

∴AF=EF，又CF=DP，

∴四边形ADEC为平行四边形；

（2）①当M点在CE上时，第一种情况：如图，当点M在CE边上时，

∵MF∥OC，

∴△EMF∽△ECO，

∴，

∵四边形MPNE为正方形，

∴MF=EF，

∴CO=EO，即4-2t=t+2，

∴t=；

第二种情况：当点N在DE边时，

∵NF∥PD，

∴△EFN∽△EPD，

∴，

∵四边形MPNE为正方形，

∴NF=EF，

∴PD=PE，即4-2t=2，

∴t=1；

∴当点M、N中有一点落在四边形ADEC的边上时，所有满足条件的t的值为t=或t=1；

②∵≤t≤1，

S=（4-2t）t=-2t2+4t=-2（t-1）2+2，

∴点M、N中恰好只有一点落在四边形ADEC的内部（不包括边界）时，≤S＜2．

关闭