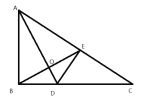
【题目】如图,将△ABC沿直线AD折叠,点B与点E重合,连接BE交AD于O.∠ABC=90°,AB=6,BC=8,AC=10,SACD=15.有下列结论:①SCDE=5;②CD=5;③OB=OE;④SABD:SACD=3:4,则以上结论正确的是( )
A. ①②B. ②③C. ②③④D. ①②③
参考答案:
【答案】B
【解析】
由题意可得△ABD≌△AED,∠AED=∠ABC=90°,AE=AB=6,则CE=4,由SACD=15可得DE=3,即可求得SCDE; 由BD= DE=3,可得CD=BC-BD=5;由△ABD≌△AED得∠BAD=∠CAD,AB=AE,由等腰三角形三线合一可得OB=OE;由SABD=![]() ,可得SABD:SACD=9:15=3:5.
,可得SABD:SACD=9:15=3:5.
解: ∵△ABC沿直线AD折叠,点B与点E重合,
∴△ABD≌△AED,
∴∠AED=∠ABC=90°,AE=AB=6,BD= DE,
∵SACD=![]() =15,AC=10,
=15,AC=10,
∴BD= DE=3,CE=AC-AE=4,
∴SCDE =![]() ,故①错误;
,故①错误;
∵△ABD≌△AED,
∴BD= DE=3,
∴CD=BC-BD=8-3=5,故②正确;
∵△ABD≌△AED,
∴∠BAD=∠CAD,AB=AE,
∴OB=OE,故③正确;
∵SABD=![]() ,SACD=15,
,SACD=15,
∴SABD:SACD=9:15=3:5,故④错误.
故以上结论正确的是②③.
故选B.
-
科目: 来源: 题型:
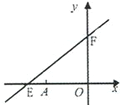
查看答案和解析>>【题目】如图,直线y=kx+6与x轴、y轴分别交于E、F.点E坐标为(-8,0),点A的坐标为(-6,0).
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为9,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB:BC:CA=3:4:5,且周长为36cm,点P从点A开始沿AB边向点B以每秒1cm的速度移动;点Q从点B沿BC边向点C以每秒2cm的速度移动;如果同时出发,则过3秒时,求△BPQ的面积。

-
科目: 来源: 题型:
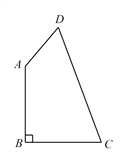
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
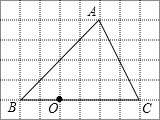
(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】为加强学生身体锻炼,某校开展体育“大课间”活动,学校决定在学生中开设A:篮球,B:立定跳远,C:跳绳,D:跑步,E:排球五种活动项目.为了了解学生对五种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的两个统计图.请结合图中的信息解答下列问题:
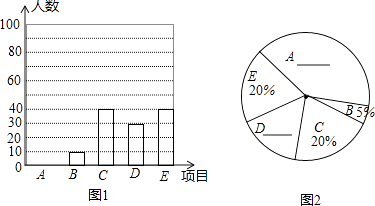
(1)在这项调查中,共调查了名学生;
(2)请将两个统计图补充完整;
(3)若该校有1200名在校学生,请估计喜欢排球的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
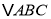 中,
中,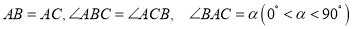 ,
,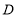 为直线
为直线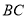 上一动点(不与点
上一动点(不与点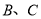 重合),在
重合),在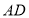 的右侧作
的右侧作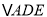 ,使得
,使得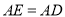 ,
,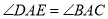 ,连接
,连接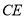 .
.(1)当点
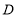 在线段
在线段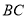 上时,求证:
上时,求证: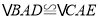 ;
;(2)当
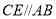 时,若点
时,若点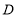 在线段
在线段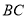 上,
上,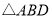 中最小角为
中最小角为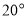 ,请求出
,请求出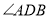 的度数;
的度数;(3)在点
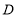 的运动过程中,当
的运动过程中,当 垂直于
垂直于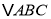 的某边时,求
的某边时,求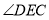 的度数(用含
的度数(用含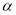 的代数式表示).
的代数式表示).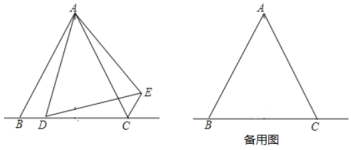
相关试题

