【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

参考答案:
【答案】(1)100;(2)补全图形见解析;(3)36°;(4)估计该校喜欢书法的学生人数为500人.
【解析】(1)用“戏曲”的人数除以其所占百分比可得;
(2)用总人数乘以“民乐”人数所占百分比求得其人数,据此即可补全图形;
(3)用360°乘以“戏曲”人数所占百分比即可得;
(4)用总人数乘以样本中“书法”人数所占百分比可得.
(1)学校本次调查的学生人数为10÷10%=100名,
故答案为:100;
(2)“民乐”的人数为100×20%=20人,
补全图形如下:
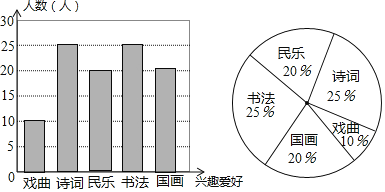
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为360°×10%=36°,
故答案为:36°;
(4)估计该校喜欢书法的学生人数为2000×25%=500人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB∥CD,EG平分∠AEF,EH⊥EG,EH∥GF,则下列结论:①EG⊥GF;②EH平分∠BEF;③FG平分∠EFC;④∠EHF=∠FEH+∠HFD;其中正确的结论个数是( )

A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
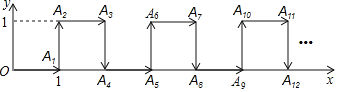
查看答案和解析>>【题目】如图,平面直角坐标系中,一个点从原点O出发,按向右→向上→向右→向下的顺序依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移到点A1,第二次移到点A2,第三次移到点A3,…,第n次移到点An,则点A2019的坐标是_____________.
-
科目: 来源: 题型:
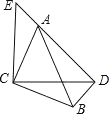
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若
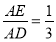 ,则
,则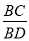 =___.
=___. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC三个顶点的坐标分别是A(-4,1),B(-1,3),C(-2,0),将三角形ABC平移得到三角形DEF,使点A与点D(1,-2)是对应点.
(1)在图中画出三角形DEF,并写出点B、C的对应点E、F的坐标;
(2)若点P在x轴上,且知三角形PCD的面积等于三角形ABC面积的
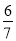 ,请写出满足条件的点P的坐标.
,请写出满足条件的点P的坐标.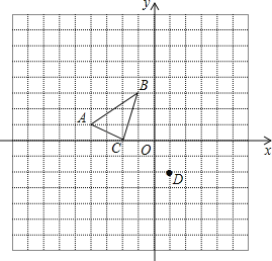
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.

相关试题

