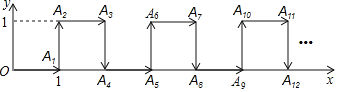
【题目】如图,平面直角坐标系中,一个点从原点O出发,按向右→向上→向右→向下的顺序依次不断移动,每次移动1个单位,其移动路线如图所示,第1次移到点A1,第二次移到点A2,第三次移到点A3,…,第n次移到点An,则点A2019的坐标是_____________.
参考答案:
【答案】(1010,1)
【解析】
观察图象可知,点A的纵坐标每4个点循环一次,由2019=505×4-1,可得点A2019的纵坐标与点A3的纵坐标相同,由A3(2,1),A7(4,1),A11(6,1)……,由此可得A4n-1(2n,1)(n为不为0的自然数),当n=505时,2n=1010,由此可得点A2019的坐标是(1010,1).
观察图象可知,点A的纵坐标每4个点循环一次,
∵2019=505×4-1,∴点A2019的纵坐标与点A3的纵坐标相同,
∵A3(2,1),A7(4,1),A11(6,1)……,
∴A4n-1(2n,1)(n为不为0的自然数),
当n=505时,2n=1010,
∴点A2019的坐标是(1010,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知用2辆A型车和1辆B型车载满货物一次可运货物10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:
(1)用1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AB∥CD,EG平分∠AEF,EH⊥EG,EH∥GF,则下列结论:①EG⊥GF;②EH平分∠BEF;③FG平分∠EFC;④∠EHF=∠FEH+∠HFD;其中正确的结论个数是( )

A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)学校这次调查共抽取了 名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“戏曲”所在扇形的圆心角度数为 ;
(4)设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?

-
科目: 来源: 题型:
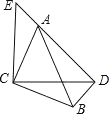
查看答案和解析>>【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若
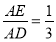 ,则
,则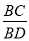 =___.
=___. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形ABC三个顶点的坐标分别是A(-4,1),B(-1,3),C(-2,0),将三角形ABC平移得到三角形DEF,使点A与点D(1,-2)是对应点.
(1)在图中画出三角形DEF,并写出点B、C的对应点E、F的坐标;
(2)若点P在x轴上,且知三角形PCD的面积等于三角形ABC面积的
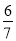 ,请写出满足条件的点P的坐标.
,请写出满足条件的点P的坐标.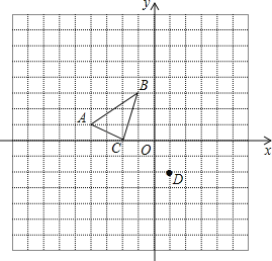
相关试题

