【题目】今年4月23日,是第16个世界读书日.某校为了解学生每周课余自主阅读的时间,在本校随机抽取若干名学生进行问卷调查,现将调查结果绘制成如图不完整的统计图表,请根据图表中的信息解答下列问题
组别 | 学习时间x(h) | 频数(人数) |
A | 0<x≤1 | 8 |
B | 1<x≤2 | 24 |
C | 2<x≤3 | 32 |
D | 3<x≤4 | n |
E | 4小时以上 | 4 |

(1)表中的n= , 中位数落在组,扇形统计图中B组对应的圆心角为°;
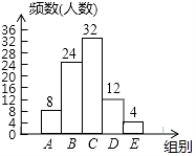
(2)请补全频数分布直方图;
(3)该校准备召开利用课余时间进行自主阅读的交流会,计划在E组学生中随机选出两人进行经验介绍,已知E组的四名学生中,七、八年级各有1人,九年级有2人,请用画树状图法或列表法求抽取的两名学生都来自九年级的概率.
参考答案:
【答案】
(1)12;C;108
(2)
解:如下图所示:
(3)
解:画树状图如下:
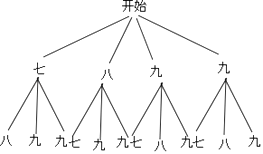
共12种可能,抽取的两名学生都来自九年级的有2种可能,
∴P(两个学生都是九年级)= ![]() =
= ![]() ,
,
答:抽取的两名学生都来自九年级的概率为 ![]() .
.
【解析】解:(1)调查的总人数为8÷10%=80,
则n=15%×80=12,
由于共有80个数据,
∴中位数为第40、41个数据的平均数,而第40、41个数据均落在C组,
∴中位数落在C组,
扇形统计图中B组对应的圆心角为 ![]() ×360°=108°,
×360°=108°,
故答案为:12,C,108;
(1)根据A组的频数和百分比求出总人数,再利用D组的百分比求出n的值,根据中位数定义即可得,圆心角=百分比×360°;(2)由(1)中n的值可得;(3)先画树状图得出所有等可能的情况数,找到抽取的两名学生都来自九年级的情况数,计算概率即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交
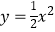 的图象于点Ai , 交直线
的图象于点Ai , 交直线 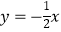 于点Bi . 则
于点Bi . 则 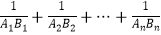 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】结算题
(1)计算:|1﹣ |+3tan30°﹣(2017﹣π)0﹣(﹣
|+3tan30°﹣(2017﹣π)0﹣(﹣  )﹣1 .
)﹣1 .
(2)已知x、y满足方程组 ,求代数式
,求代数式 
 ﹣
﹣  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=ax﹣a(a为常数)的图象与y轴相交于点A,与函数
 的图象相交于点B(m,1).
的图象相交于点B(m,1). 
(1)求点B的坐标及一次函数的解析式;
(2)若点P在y轴上,且△PAB为直角三角形,请直接写出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务需要多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.

(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.

(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、N、G为顶点的四边形是正方形时,请求出点M的坐标.
相关试题

