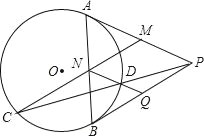
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
参考答案:
【答案】见解析
【解析】试题分析:连接OA,OB,OC,OD,OP. 由![]() 是
是![]() 的中点,根据三角形中位线的性质,可得MN∥BP.,又由PA、PB为
的中点,根据三角形中位线的性质,可得MN∥BP.,又由PA、PB为![]() 的切线,可得AB⊥OP.可证得NM=MP,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得
的切线,可得AB⊥OP.可证得NM=MP,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得
MP∥NQ,则可得四边形MNQP是平行四边形,证得四边形MNQP是菱形.
试题解析:证明:连接OA,OB,OC,OD,OP.
∵AN=NB,AM=MP.
∴MN∥BP.
∵PA、PB为![]() 的切线,
的切线,
∴AB⊥OP.
∴NM=MP,∠MNP=∠MPN,
在Rt△AOP中,由射影定理,得![]()
由切割线定理,得![]()
∴PNPO=PDPC,
∴O,C,D,N四点共圆,
∴∠PND=∠OCD,∠ONC=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠MNP=∠ONC,
∴∠MNP=∠PND=∠MPN,
∴MP∥NQ,
∴四边形MNQP是平行四边形,
∴四边形MNQP是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的
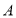 型智能手表,去年销售总额为80000元,今年
型智能手表,去年销售总额为80000元,今年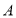 型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少
型智能手表的售价每只比去年降了600元,若今年售出的数量与去年相同的情况下,今年的销售总额将比去年减少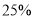 .
.(1)求今年
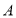 型智能手表每只售价多少元?
型智能手表每只售价多少元?(2)今年这家代理商准备新进一批
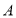 型智能手表和
型智能手表和 型智能手表共100只,它们的进货价与销售价格如下表所示,若
型智能手表共100只,它们的进货价与销售价格如下表所示,若 型智能手表进货量不超过
型智能手表进货量不超过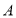 型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
型智能手表进货量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?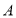 型智能手表
型智能手表 型智能手表
型智能手表进价
1300元/只
1500元/只
售价
今年的售价
2300元/只
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上,点O为原点,点A对应的数为9,点B对应的数为b,点C在点B右侧,长度为2个单位的线段BC在数轴上移动.
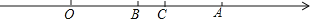
(1)如图,当线段BC在O、A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)当线段BC在数轴上沿射线AO方向移动的过程中,若存在AC﹣OB=
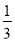 AB,求此时满足条件的b的值;
AB,求此时满足条件的b的值;(3)当线段BC在数轴上移动时,满足关系式|AC﹣OB|=
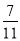 |AB﹣OC|,则此时b的取值范围是
|AB﹣OC|,则此时b的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所知道的四边形中是勾股四边形的两种图形的名称_____,_____;
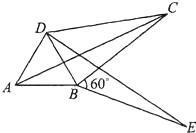
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,连接AD、DC,若∠DCB=30°,试证明;DC2+BC2=AC2.(即四边形ABCD是勾股四边形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月初某地猪肉价格大幅度下调,下调后每千克猪肉的价格是原价格的
 ,原来用120元买到的猪肉下调后可多买2kg.4月中旬猪肉价格开始回升,经过两个月后,猪肉价格上调为每千克28.8元.
,原来用120元买到的猪肉下调后可多买2kg.4月中旬猪肉价格开始回升,经过两个月后,猪肉价格上调为每千克28.8元.(1)求4月初猪肉价格下调后变为每千克多少元.
(2)求5、6月份猪肉价格的月平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
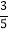 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)求直线OA和二次函数的解析式;
(2)当点P在直线OA的上方时,
①当PC的长最大时,求点P的坐标;
②当S△PCO=S△CDO时,求点P的坐标.


相关试题

