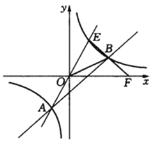
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A、E,AB交双曲线于另一点B(
交于点A、E,AB交双曲线于另一点B(![]() ,
,![]() ),连接EB并延长交x轴于点F.
),连接EB并延长交x轴于点F.
(1)![]() ;
;
(2)求直线AB的解析式;
(3)求△EOF的面积;
(4)若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.
参考答案:
【答案】(1)2;(2)y=x-2;(3)12;(4)(-4,-2)或(0,-6)或(8,10)
【解析】
(1)把B(![]() ,
,![]() )代入反比例函数
)代入反比例函数![]() 即可求出m的值;
即可求出m的值;
(2)联立直线y=2x与反比例函数![]() 即可求出A,E坐标,然后用待定系数法确定直线AB的关系式;
即可求出A,E坐标,然后用待定系数法确定直线AB的关系式;
(3)先用待定系数法求出EB的解析式,再令y=0,得出F的坐标,最后用三角形的面积公式求出△EOF的面积;
(4)分类讨论:分别以AB,BE,AE为对角线求对应的P的坐标.
(1)∵点B(2m,m)在反比例函数![]() 上,
上,
∴2m·m=8,解得m=±2,而m>0,
∴m=2
(2)m=2,则点B的坐标为(4,2)
联立解析式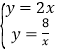 得
得![]() 或
或![]()
∴点A坐标为(-2,-4),E点坐标为(2,4)
设直线AB的解析式为y=k1x+b1,
把A(-2,-4),B(4,2)代入得:-2k1+b1=-4,4k1+b1=2,
解方程组得k1=1, b1=-2,
∴直线AB的解析式为y=x-2;
(3)设直线EB的解析式为y=k2x+b2,
把E(2,4),B(4,2)代入可得2k2+b2=4,4k2+b2=2,解得k2=-1,b2=6,
∴直线EB的解析式为y=-x+6,
令y=0,解得x=6,故F(6,0)
∴S△EOF=![]() =12
=12
(4)①以AB为对角线时,由A(-2,-4),B(4,2)求出中点O坐标为(1,-1),故E(2,4)关于中点O(1,-1)的对称点P为(0,-6);
②以BE为对角线时,由E(2,4),B(4,2)求出中点O’坐标为(3,3),故A(-2,-4)关于中点O’(3,3)的对称点P为(8,10);
③以AE为对角线时,由A(-2,-4),E(2,4)求出中点O’坐标为(0,0),故B(4,2)关于中点O’(0,0)的对称点P为(-4,-2);
故满足条件的点P的坐标为(-4,-2)或(0,-6)或(8,10)
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.

完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年4月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况. 我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:

(1)请将两幅图补充完整;
(2)在这次形体测评中,一共抽查了______名学生,如果全市有20万名初中生,那么全市初中生中,三姿良好的学生约有______人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=2x-2的图像与反比例函数y=
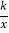 的图像交于点M(2,a)与N(b,-4)两点。
的图像交于点M(2,a)与N(b,-4)两点。(1)求反比例函数的解析式.
(2)画出草图,根据图像写出反比例函数的值大于一次函数的值时的x的取值范围.
(3)求△MON的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2011次运动后,动点P的坐标是____________。

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)解方程组:
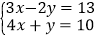 .
.(2)解不等式组
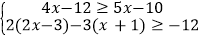 (并把解集在数轴上表示出来).
(并把解集在数轴上表示出来). -
科目: 来源: 题型:
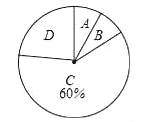
查看答案和解析>>【题目】今年10月,某公司随机抽取所属的a家连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.

根据以上信息解答下列问题:
(1)求a的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
相关试题

