【题目】一般地,二元一次方程的解可以转化为点的坐标,其中x的值对应为点的横坐标,y的值对应为点的纵坐标,如二元一次方程x2y=0的解![]() 和
和![]() 可以转化为点的坐标A(0,0)和B(2,1).以方程x2y=0的解为坐标的点的全体叫做方程x2y=0的图象。
可以转化为点的坐标A(0,0)和B(2,1).以方程x2y=0的解为坐标的点的全体叫做方程x2y=0的图象。

(1)写出二元一次方程x2y=0的任意一组解___,并把它转化为点C的坐标___;
(2)在平面直角坐标系中,任何一个二元一次方程的图象都是一条直线,如方程x2y=0的图象是由该方程所有的解转化成的点组成,在图中描出点A. 点B和点C,观察它们是否在同一直线上;
(3)取满足二元一次方程x+y=3的两个解,并把它们转化成点的坐标,画出二元一次方程x+y=3的图象;
(4)根据图象,写出二元一次方程x2y=0的图象和二元一次方程x+y=3的图象的交点坐标___,由此可得二元一次方程组![]() 的解是___.
的解是___.
参考答案:
【答案】(1)![]() ,(2,1);(2)见解析;(3)见解析;(4) (2,1),
,(2,1);(2)见解析;(3)见解析;(4) (2,1),![]()
【解析】
(1)计算出x=-2所对应的y的值即可得到方程的一组解,然后把它转化为点C的坐标;
(2)利用描点法画直线AB,然后利用画的直线可判断点C在直线AB上;
(3)取两组对应值,然后利用描点法画直线x+y=3即可;
(4)利用画出的图象写出交点坐标,然后利用方程组的解就是两个相应的函数图象的交点坐标求解.
(1)二元一次方程x2y=0的解可为![]() ,把它转化为点C的坐标为(2,1);
,把它转化为点C的坐标为(2,1);
(2)如图,点A. 点B和点C同一直线上;
(3)二元一次方程x+y=3的两个解为![]() 或
或![]() ,把它们转化成点的坐标为(3,0),(0,3),如图;
,把它们转化成点的坐标为(3,0),(0,3),如图;
(4)根据图象,二元一次方程x2y=0的图象和二元一次方程x+y=3的图象的交点坐标为(2,1),由此可得二元一次方程组![]() 的解是
的解是![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来, ,于是可用
,于是可用 来表示
来表示 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:(1)
 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.(2)如果
 的小数部分为
的小数部分为 ,
, 的整数部分为
的整数部分为 ,求
,求 的值.
的值.(3)已知:
 ,其中
,其中 是整数,且
是整数,且 ,求
,求 的相反数.
的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,E、F 是平行四边形 ABCD 的对角线 AC 上的两点,AE=CF.

求证:(1)EB DF ;
(2)EB∥DF .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某供暖部门为了解市民对2016年供暖情况的满意程度,对若干户市民进行了抽样调查(把市民对供暖情况的满意程度分为三个层次,A层次:满意;B层次:比较满意;C层次:不满意),将调查结果绘制成了如图所示的条形统计图和扇形统计图.
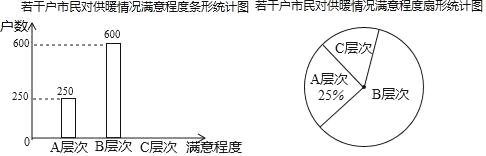
(1)请计算多少户市民参加了此次抽样调查,并补全条形统计图.
(2)根据抽样调查结果,请估计16000户市民中大约有多少户对2016年的供暖情况满意和比较满意.(包括A层次和B层次)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,反映的是九(1)班学生外出乘车、步行、骑车的人数直方图的一部分和圆形分布图,下列说法:①九(1)班外出步行有8人;②在圆形统计图中,步行人数所占的圆心角度数为82°;
③九(1)班外出的学生共有40人;④若该校九年级外出的学生共有500人,那么估计全年级外出骑车的人约有150人,其中正确的结论是( )


A. ①②③ B. ①③④ C. ②③ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,后解答:
(1)由根式的性质计算下列式子得:
①
 =3,②
=3,② ,③
,③ ,④
,④ =5,⑤
=5,⑤ =0.
=0.由上述计算,请写出
 的结果(a为任意实数).
的结果(a为任意实数).(2)利用(1)中的结论,计算下列问题的结果:
①
 ;
;②化简:
 (x<2).
(x<2).(3)应用:
若
 =3,求x的取值范围.
=3,求x的取值范围.
相关试题

