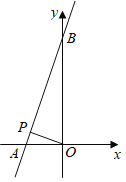
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,与
,与![]() 轴交点为
轴交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)若点![]() 为线段
为线段![]() 上的一个动点,
上的一个动点,![]() 为坐标原点,是否存在点
为坐标原点,是否存在点![]() ,使
,使![]() 的值最小?若存在,求出
的值最小?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
参考答案:
【答案】(1)![]()
![]() ,
,![]()
![]() ;(2)存在,
;(2)存在,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)在一次函数![]() 中,分别令
中,分别令![]() 和
和![]() ,解相应方程,可求得A、B两点的坐标;
,解相应方程,可求得A、B两点的坐标;
(2)由垂线段最短可知当![]() 时,OP最小,利用面积法求出OP长即可.
时,OP最小,利用面积法求出OP长即可.
解:(1)![]() 一次函数
一次函数![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,![]() 点A坐标为
点A坐标为![]() ,点B坐标为
,点B坐标为![]() ;
;
(2)存在点P使得OP的值最小,理由如下:![]() 点P为线段AB上一个动点,O为坐标原点,
点P为线段AB上一个动点,O为坐标原点,![]() 当OP最小时满足
当OP最小时满足![]() ,此时OP即为
,此时OP即为![]() 中AB边上的高,
中AB边上的高,![]() 取得最小值,
取得最小值,点A坐标为
![]() ,点B坐标为
,点B坐标为![]() ,
,![]() ,
,![]() ,
,![]() 由勾股定理得:
由勾股定理得:![]() ,
,![]() 的面积
的面积![]() ,
,![]() ,
,![]() 存在点P使OP的值最小,此时
存在点P使OP的值最小,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市对教师试卷讲评课中学生参与的深度与度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项,评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有
 万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人.
万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人.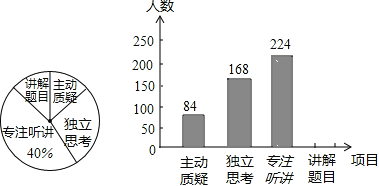
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
(1)如图1,当∠ABE=45°,c=2
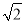 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
(3)如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2
 ,AB=3.求AF的长.
,AB=3.求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC与△DEF中,给出下列六个条件:(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个条件为已知,不能判断△ABC与△DEF全等的是( )
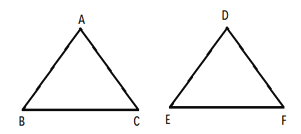
A. (1)(2)(3)B. (1)(2)(5)
C. (1)(4)(6)D. (2)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是_______________________;中线AD的取值范围是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.

(1)求抛物线的解析式;
(2)当0<t≤8时,求△APC面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:
①若a>0,b>0,则a+b>0;
②若a2=b2,则a=b;
③线段垂直平分线上的点到线段两端点距离相等;
④平行四边形的对角线互相平分
其中原命题与逆命题均为真命题的是( )
A. ①③ B. ②④ C. ③④ D. ②③
相关试题

