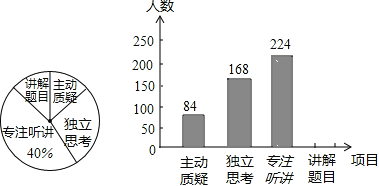
【题目】我市对教师试卷讲评课中学生参与的深度与度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项,评价组随机抽取了若干名初中学生的参与情况,绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形图补充完整;
(3)如果全市有![]() 万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人.
万名初中学生,那么在试卷评讲课中,“独立思考”的学生约有多少万人.
参考答案:
【答案】(1)560;(2)答案见解析;(3)0.48万人.
【解析】
(1)用专注听讲的人数224除以专注听讲所占的百分比即可得到所抽查的学生总人数;
(2)根据所抽查的学生四项人数总和求出讲解题目的人数,再补全图形即可;
(3)用16万乘以“独立思考”的学生所占的百分比即可.
解:(1)抽查的学生总人数![]() 名
名![]() ;
;
故答案为560;
(2)讲解题目的人数![]() 名
名![]() ,
,
画条形统计图为:
(3)![]() 万
万![]() ,
,![]() 全市在试卷讲评课中,“独立思考”的学生约有
全市在试卷讲评课中,“独立思考”的学生约有![]() 万人.
万人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.

(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.比如在学习“同底数幂的乘法法则”过程中,利用有理数的乘方概念和乘法结合律,可由“特殊”抽象概括出“一般”,具体如下22×23=25,23×24=27,22×26=28…→2m2n=2m+n…→aman=am+n(m、n都是正整数)我们亦知:
 ,
,  ,
,  ,
,  …
…(1)请你根据上面的材料,用字母a、b、c归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式.
(2)请尝试说明(1)中关系式的正确性.
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图4所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,

若∠1:∠2:∠3=28:5:3,则∠α的度数是 ( )
A. 80° B. 100° C. 60° D. 45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
(1)如图1,当∠ABE=45°,c=2
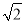 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
(3)如图4,在ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2
 ,AB=3.求AF的长.
,AB=3.求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC与△DEF中,给出下列六个条件:(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F,以其中三个条件为已知,不能判断△ABC与△DEF全等的是( )
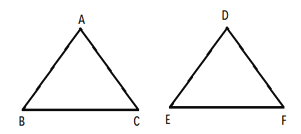
A. (1)(2)(3)B. (1)(2)(5)
C. (1)(4)(6)D. (2)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
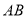 的函数表达式为
的函数表达式为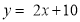 ,与
,与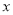 轴交点为
轴交点为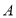 ,与
,与 轴交点为
轴交点为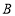 .
.(1)求
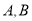 两点的坐标;
两点的坐标;(2)若点
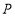 为线段
为线段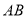 上的一个动点,
上的一个动点,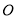 为坐标原点,是否存在点
为坐标原点,是否存在点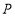 ,使
,使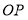 的值最小?若存在,求出
的值最小?若存在,求出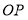 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.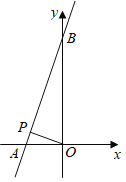
相关试题

