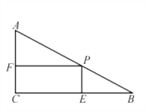
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=12cm,点P是AB边上的一个动点,过点P作PE⊥BC于点E,PF⊥AC于点F,当PB=6cm时,四边形PECF的面积最大,最大值为______
参考答案:
【答案】9![]() cm2
cm2
【解析】试题分析:设PE=x,在Rt△PEB中,根据∠B=30°,可知PB=2x,BE=![]() x,再在Rt△ABC中,利用三角函数的知识求出BC的长,进而可以表示出CE的长度;然后利用矩形的面积公式,即可得到四边形PECF的面积S关于x的表达式,对表达式进行配方,利用二次函数的最值即可得到答案.
x,再在Rt△ABC中,利用三角函数的知识求出BC的长,进而可以表示出CE的长度;然后利用矩形的面积公式,即可得到四边形PECF的面积S关于x的表达式,对表达式进行配方,利用二次函数的最值即可得到答案.
解:设PE=x,由∠B=30°,
得PB=2x,BE=![]() x.
x.
由AB=12cm,
得BC=12×cos30°=6![]() cm,
cm,
故CE=BC-BE=6![]() -
-![]() x.
x.
则四边形PECF的面积=CE×PE=(6![]() -
-![]() x)x=-
x)x=-![]() x2+6
x2+6![]() x=-
x=-![]() (x-3)2+9
(x-3)2+9![]() ,
,
当x=3cm,即PB=2x=6cm时,四边形PECF的面积最大,最大值是9![]() cm2.
cm2.
故答案为:9![]() cm2.
cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋子中装有除颜色外都相同的6个红球和4个黄球,从袋子中任意摸出一个球,请问:
(1)“摸出的球是白球”是什么事件?
(2)“摸出的球是红球”是什么事件?
(3)“摸出的球不是绿球”是什么事件?
(4)摸出哪种颜色球的可能性最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:

(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
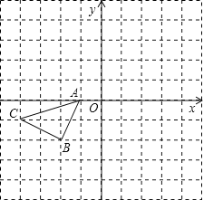
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△AB1C1关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器超市销售每台进价分别为160元,200元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段
销售数量
销售收入/元
A种型号/台
B种型号/台
第1周
3
5
1800
第2周
4
10
3200
(1)A、B两种型号的电风扇的销售单价是多少?
(2)若该超市准备用不多于5400元的金额再次采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:

(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问采用何种购买方案可以使得每月处理污水量的吨数为最多?并求出最多吨数.
相关试题

