【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
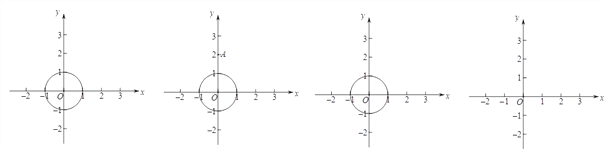
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;
若点P在直线x = 2上,则点P关于⊙O的最大“视角”的度数 ;
②在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标;
③若点P在直线![]() 上,且点P关于⊙O的“视角”大于60°,求点P的横坐标
上,且点P关于⊙O的“视角”大于60°,求点P的横坐标![]() 的取值范围.
的取值范围.
(2)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,-1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)①画图见解析;②B(![]() ,
, ![]() )③0<
)③0<![]() <
<![]() (2)
(2)![]() <
<![]() 或
或![]() >
>![]() .
.
【解析】(1)①如图1中,过点A作⊙O的切线,切点分别为M、N. 点A关于⊙O的“视角”就是两条切线的夹角,∠MAN就是点P在直线x = 2关于⊙O的“视角”;②由①可知,点A关于⊙O的“视角”为60°,根据对称性即可推出点B的坐标;由点P在直线![]() 上,从而可求出点P的横坐标
上,从而可求出点P的横坐标![]() 的取值范围.
的取值范围.
(2)当⊙C的圆心在x轴上,设切点为P,连接PC则PC⊥AP,想办法求出点C的坐标,求出此时的点C坐标,即可解决问题.
解:(1)①画图

60°
②∵点B关于⊙O的视角为60°,
∴点B在以O为圆心,2为半径的圆上,即OB=2
∵B(m,m) (m>0),
∴OB=![]() ,
,
∴![]() .
.
∴B(![]() ,
, ![]() )
)
③∵点P关于⊙O的“视角”大于60°,
∴点P在以O为圆心1为半径与2为半径的圆环内.
∵点P在直线![]() 上,由上可得
上,由上可得![]() =0或
=0或 ![]()
∴0<![]() <
< ![]()
(2)![]() <
<![]() 或
或![]() >
>![]() .
.
“点睛”本题考圆综合题、切线的性质、一次函数的应用,解题的关键是理解题意,灵活应用所学知识解决问题,学会添加常用辅助线,学会寻找特殊位置解决问题,属于中考压轴题./span>
-
科目: 来源: 题型:
查看答案和解析>>【题目】在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是_____(只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=
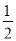 时, 若CD=
时, 若CD= ,求AD长.
,求AD长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12、10、15、
8,则第5组的频率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程有两个相等的实数根的是( )
A.x2+1=0
B.x2+4x﹣4=0
C.x2+x+ =0
=0
D.x2﹣x+ =0
=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中能用提公因式法分解因式的是( )
A. x2-y2 B. x2+y2 C. x2+2x D. x2-xy+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列给出的四个命题:
①若|a|=|b|,则a|a|=b|b|;②若a2﹣5a+5=0,则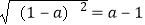 ;③(a﹣1)
;③(a﹣1) 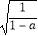 =
= 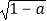
④若方程x2+px+q=0的两个实根中有且只有一个根为0,那么p≠0,q=0.
其中是真命题是( )
A.①②
B.②③
C.②④
D.③④
相关试题

