【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD=![]() 时, 若CD=
时, 若CD=![]() ,求AD长.
,求AD长.

参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】(1)由四边形ABCD为平行四边形得出AD//BC,证得△BEF∽△DAF即可得出结论;
(2)在Rt△ABF中,利用勾股定理求出AB、DF 即可得到AD的长.
(1)证明:∵四边形ABCD为平行四边形
∴AD//BC,AD=BC,AB=CD
∵点E为BC的中点
∴BE=![]() BC=
BC=![]() A D
A D
∵AD//BC,∴△BEF∽△DAF
∴![]()
∴DF=2BF
(2)解:∵CD=![]()
∴AB=CD=![]()
∵在Rt△ABF中,∠AFB=90°
![]()
∴设AF=x,则BF=2x
∴AB = ![]() =
=![]() , x =
, x =![]()
∴x=1,AF=1,BF=2
∵DF=2BF
∴DF=4
∴ AD = ![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若⊙O1、⊙O2的半径分别为4和6,圆心距O1O2=8,则⊙O1与⊙O2的位置关系是( )
A.内切
B.相交
C.外切
D.外离 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(a,3)与点Q(﹣2,b)关于原点对称,则a﹣b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是_____(只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学测试后,某班50名学生的成绩被分为5组,第1~4组的频数分别为12、10、15、
8,则第5组的频率是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;
若点P在直线x = 2上,则点P关于⊙O的最大“视角”的度数 ;
②在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标;
③若点P在直线
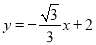 上,且点P关于⊙O的“视角”大于60°,求点P的横坐标
上,且点P关于⊙O的“视角”大于60°,求点P的横坐标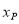 的取值范围.
的取值范围.(2)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,-1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标
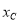 的取值范围.
的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程有两个相等的实数根的是( )
A.x2+1=0
B.x2+4x﹣4=0
C.x2+x+ =0
=0
D.x2﹣x+ =0
=0
相关试题

