【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

参考答案:
【答案】(1)2(2)当点P、Q运动时,线段DE的长度不会改变。理由见解析
【解析】解:(1)∵△ABC是边长为6的等边三角形,∴∠ACB=60°。
∵∠BQD=30°,∴∠QCP=90°。
设AP=x,则PC=6﹣x,QB=x,∴QC=QB+C=6+x。
∵在Rt△QCP中,∠BQD=30°,∴PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),解得x=2。
(6+x),解得x=2。
∴当∠BQD=30°时,AP=2。
(2)当点P、Q运动时,线段DE的长度不会改变。理由如下:
作QF⊥AB,交直线AB的延长线于点F,连接QE,PF。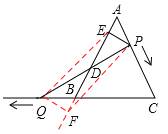
∵PE⊥AB于E,∴∠DFQ=∠AEP=90°。
∵点P、Q做匀速运动且速度相同,∴AP=BQ。
∵△ABC是等边三角形,∴∠A=∠ABC=∠FBQ=60°。
∴在△APE和△BQF中,
∵∠A=∠FBQ,AP=BQ,∠AEP=∠BFQ=90°,∴△APE≌△BQF(AAS)。
∴AE=BF,PE=QF且PE∥QF。∴四边形PEQF是平行四边形。
∴DE=![]() EF。
EF。
∵EB+AE=BE+BF=AB,∴DE=![]() AB。
AB。
又∵等边△ABC的边长为6,∴DE=3。
∴当点P、Q运动时,线段DE的长度不会改变。
(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QCP=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC=![]() QC,即6﹣x=
QC,即6﹣x=![]() (6+x),求出x的值即可。
(6+x),求出x的值即可。
(2)作QF⊥AB,交直线AB的延长线于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=![]() AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变。
AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变。
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并求出所有正整数解的和.
,并求出所有正整数解的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于2100元,则第二批衬衫每件至少要售多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在当今“互联网
 ”时代,有一种用“因式分解法”生成密码的方法:将一个多项式因式分解,如将多项式
”时代,有一种用“因式分解法”生成密码的方法:将一个多项式因式分解,如将多项式 分解的结果为
分解的结果为 当
当 时,
时, ,
, ,
, ,此时可得到数字密码182021.
,此时可得到数字密码182021. 根据上述方法,当
根据上述方法,当 ,
, 时,对于多项式
时,对于多项式 分解因式后可以形成哪些数字密码
分解因式后可以形成哪些数字密码 写出两个即可
写出两个即可 ?
? 将多项式
将多项式 因式分解后,利用题目中所示的方法,当
因式分解后,利用题目中所示的方法,当 时可以得到密码808890,求m,n的值.
时可以得到密码808890,求m,n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为( )
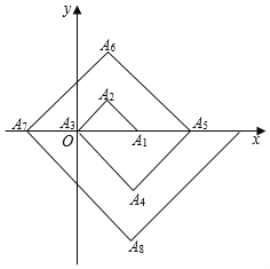
A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间/(单位:min),然后利用所得数据绘制成如下不完整的统计图表.

根据图表中提供的信息,回答下列问题:
(1)a=_____,b=_____;
(2)将频数分布直方图补充完整;
(3)若该校共1 000名学生,估计有多少学生平均每天的课外阅读时间不少于50min?
相关试题

