【题目】如图,在平面直角坐标系中,函数y=2x+8的图象分别交x轴、y轴于A、B两点,过点A的直线交y轴正半轴于点M,且点M为线段OB的中点.

(1)求直线AM的函数解析式.
(2)试在直线AM上找一点P,使得S△ABP=S△AOB,求出点P的坐标.
(3)若点H为坐标平面内任意一点,在坐标平面内是否存在这样的点H,使以A、B、M、H为顶点的四边形是平行四边形?若存在,请直接写出所有点H的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x+4;(2)点P的坐标为(-12,-8)或(4,8);(3)存在,(-4,-4),(-4,4)或(4,12).
【解析】
(1)通过函数y=2x+8求出A、M两点坐标,由两点坐标求出直线AM的函数解析式;
(2)设出P点坐标,按照等量关系“S△ABP=S△AOB”即可求出;
(3)设点H的坐标为(m,n),然后分三种情况进行讨论即可.
(1)当x=0时,y=2x+8=8,
∴点B的坐标为(0,8);
当y=0时,2x+8=0,
解得:x=-4,
∴点A的坐标为(-4,0).
∵点M为线段OB的中点,
∴点M的坐标为(0,4).
设直线AM的函数解析式为y=kx+b(k≠0),
将A(-4,0),B(0,4)代入y=kx+b,得:![]() ,
,
解得:![]() ,
,
∴直线AM的函数解析式为y=x+4.
(2)设点P的坐标为(x,x+4),
∵S△ABP=S△AOB,
∴![]() BM|xP-xA|=
BM|xP-xA|=![]() OAOB,即
OAOB,即![]() ×4×|x+4|=
×4×|x+4|=![]() ×4×8,
×4×8,
解得:x1=-12,x2=4,
∴点P的坐标为(-12,-8)或(4,8).
(3)存在, (-4,-4),(-4,4)或(4,12).
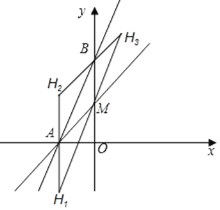
设点H的坐标为(m,n).
分三种情况考虑(如图所示):
①当AM为对角线时,![]() ,
,
解得:![]() ,
,
∴点H1的坐标为(-4,-4);
②当AB为对角线时, ![]() ,
,
解得:![]() ,
,
∴点H2的坐标为(-4,4);
③当BM为对角线时,![]() ,
,
解得:![]() ,
,
∴点H3的坐标为(4,12).
综上所述:在坐标平面内存在点H,使以A、B、M、H为顶点的四边形是平行四边形,点H的坐标为(-4,-4),(-4,4)或(4,12).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家______ 千米,张强从家到体育场用了______ 分钟;
(2)体育场离文具店______ 千米;
(3)张强在文具店逗留了______ 分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是( )

A. ②④ B. ①③ C. ②③④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2台大收割机和5台小收割机同时工作2 h共收割小麦3.6hm2,3台大收割机和2台小收割机同时工作5 h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=
 x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在节日期间开展优惠促销活动:凡购买原价超过200元的商品,超过200元的部分可以享受打折优惠若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)之间的函数关系的a图象如图所示,则图中a的值是( )
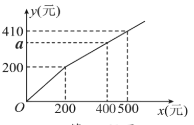
A.300B.320C.340D.360
相关试题

