【题目】如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求一次函数的解析式;
(2)判断点C(4,-2)是否在该一次函数的图象上,说明理由;
(3)若该一次函数的图象与x轴交于D点,求△BOD的面积.

参考答案:
【答案】(1)y=-x+3;(2)不在,理由见解析;(3)3
【解析】(1)首先求得B的坐标,然后利用待定系数法即可求得函数的解析式;
(2)把C的坐标代入一次函数的解析式进行检验即可;
(3)首先求得D的坐标,然后利用三角形的面积公式求解.
解:(1)在y=2x中,令x=1,得y=2,则点B的坐标是(1,2),
设一次函数的解析式是y=kx+b(k≠0),
则![]() 解得
解得![]()
故一次函数的解析式是y=-x+3.
(2)点C(4,-2)不在该一次函数的图象上.
理由:对于y=-x+3,当x=4时,y=-1≠-2,
所以点C(4,-2)不在该函数的图象上.
(3)在y=-x+3中,令y=0,得x=3,则点D的坐标是(3,0),
则S△BOD=![]() ×OD×2=
×OD×2=![]() ×3×2=3.
×3×2=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,中俄“海上联合—2017”军事演习在海上编队演习中,两艘航母护卫舰从同一港口O同时出发,一号舰沿南偏西30°方向以12海里/小时的速度航行,二号舰以16海里/小时速度航行,离开港口1.5小时后它们分别到达A,B两点,相距30海里,则二号舰航行的方向是( )

A. 南偏东30° B. 北偏东30° C. 南偏东 60° D. 南偏西 60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC的垂直平分线分别交AB,CD于点E,F,连接AF,CE,如果∠BCE=26°,则∠CAF=_____

-
科目: 来源: 题型:
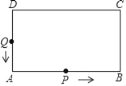
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=14cm,AD=8cm,动点P沿AB边从点A开始,向点B以1cm/s的速度运动;动点Q从点D开始沿DA→AB边,向点B以2cm/s的速度运动.P,Q同时开始运动,当点Q到达B点时,点P和点Q同时停止运动,用t(s)表示运动的时间.
(1)当点Q在DA边上运动时,t为何值,使AQ=AP?
(2)当t为何值时,AQ+AP等于长方形ABCD周长的
 ?
?(3)当t为何值时,点Q能追上点P?
-
科目: 来源: 题型:
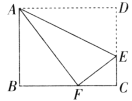
查看答案和解析>>【题目】如图,折叠矩形纸片的一边AD,使点D落在BC边上的点F处,BC=10cm, AB=8cm, 则EC的长为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上,点O为原点,点A对应的数为11,点B对应的数为b,点C在点B右侧,长度为3个单位的线段BC在数轴上移动,
(1)如图1,当线段BC在O,A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)线段BC在数轴上沿射线AO方向移动的过程中,是否存在AC﹣OB=
 AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
-
科目: 来源: 题型:
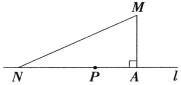
查看答案和解析>>【题目】如图,一学校(点M)距公路(直线l)的距离(MA)为1km,在公路上距该校2km处有一车站(点N),该校拟在公路上建一个公交车停靠点(点p),以便于本校职工乘车上下班,要求停靠站建在AN之间且到此校与车站的距离相等,请你计算停靠站到车站的距离.
相关试题

