【题目】把一副三角板的直角顶点O重叠在一起.
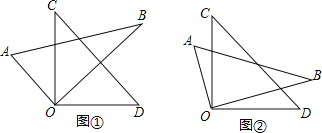
(1)问题发现:如图①,当OB平分∠COD时,∠AOD+∠BOC的度数是 ;
(2)拓展探究:如图②,当OB不平分∠COD时,∠AOD+∠BOC的度数是多少?
(3)问题解决:当∠BOC的余角的4倍等于∠AOD时,求∠BOC的度数.
参考答案:
【答案】(1)180°;(2)180°;(3)60°.
【解析】
试题分析:(1)先根据OB平分∠COD得出∠BOC及∠AOC的度数,进而可得出结论;
(2)根据直角三角板的性质得出∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°进而可得出结论;
(3)根据(1)、(2)的结论可知∠AOD+∠BOC=180°,故可得出∠AOD=180°﹣∠BOC,根据∠BOC的余角的4倍等于∠AOD即可得出结论.
解:(1)∵OB平分∠COD,
∴∠BOC=∠BOD=45°.
∵∠AOC+∠BOC=45°,
∴∠AOC=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°.
故答案为:180°;
(2)∵∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+∠BOC=90°,
∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=90°+90°=180°;
(3)∵由(1)、(2)得,∠AOD+∠BOC=180°,
∴∠AOD=180°﹣∠BOC.
∵∠AOD=4(90°﹣∠BOC),
∴180°﹣∠BOC=4(90°﹣∠BOC),
∴∠BOC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
甲种糖果
乙种糖果
丙种糖果
单价(元/千克)
15
25
30
千克数
40
40
20
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
-
科目: 来源: 题型:
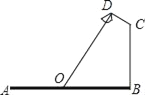
查看答案和解析>>【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A. (11﹣2
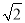 )米 B. (11
)米 B. (11 ﹣2
﹣2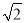 )米 C. (11﹣2
)米 C. (11﹣2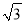 )米 D. (11
)米 D. (11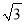 ﹣4)米
﹣4)米 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从①
 ,②
,② ,③
,③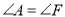 三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
三个条件中选出两个作为已知条件,另一个作为结论可以组成3个命题.
(1)这三个命题中,真命题的个数为________;
(2)选择一个真命题,并且证明.(要求写出每一步的依据)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊿ABC中,∠A=40°,∠ACB=104°,BD为AC边上的高,BE是⊿ABC的角平分线,求∠EBD的度数.
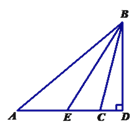
【答案】32°
【解析】试题分析:根据三角形的内角和定理求出∠ABC,再根据角平分线的定义求出∠ABE,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式求出∠BED,再根据直角三角形两锐角互余列式进行计算即可得解.
试题解析:由三角形内角和定理,得∠B+∠ACB+∠BAC=180°,
又∠A=40°,∠ACB=104°,
∴∠ABC=180°-40°-104°=36°,
又∵BE平分∠ABC,
∴∠ABE=
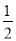 ∠ABC=18°
∠ABC=18°∴∠BED=∠A+∠ABE=40°+18°=58°,
又∵∠BED+∠DBE=90°,
∴∠DBE=90°-∠BED=90°-58°=32°.
【题型】解答题
【结束】
25【题目】已知,如图, AB∥CD,∠1=∠2,那么∠E和∠F相等吗? 为什么?
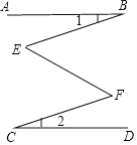
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某农户想建造一花圃,用来种植两种不同的花卉,以供应城镇市场需要,现用长为36m的篱笆,一面砌墙(墙的最大可使用长度l=13m),围成中间隔有一道篱笆的长方形花圃,设花圃宽AB为x,面积为S.
(1)求S与x的函数关系式.并指出它是一次函数,还是二次函数?
(2)若要围成面积为96m2的花圃,求宽AB的长度.
(3)花圃的面积能达到108m2吗?若能,请求出AB的长度,若不能请说明理由.
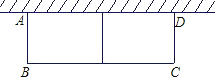
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
探究发现:如图所示,小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为(a+b)的正方形(其中a、b的和不变,但a、b的数值及两者的大小关系都可以变化).仔细观察拼图,我们发现,如果右图中间有空白图形F,那么它一定是正方形
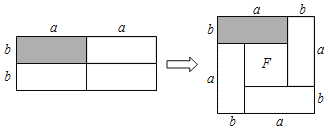
(1)空白图形F的边长为 ;
(2)通过计算左右两个图形的面积,我们发现(a+b)2、(a﹣b)2和ab之间存在一个等量关系式.
①这个关系式是 ;
②已知数x、y满足:x+y=6,xy=
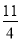 ,则x﹣y= ;
,则x﹣y= ;问题解决:
问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
①对于周长一定的长方形,设周长是20,则长a和宽b的和是 面积S=ab的最大值为 ,此时a、b的关系是 ;
②对于周长为L的长方形,面积的最大值为 .
活动经验:
周长一定的长方形,当邻边长度a、b满足 时面积最大.
相关试题

