【题目】已知一次函数y=kx+b(![]() )与y=-4x(
)与y=-4x(![]() )的图像相交于点P(1,n),且C(3,2)在一次函数图像上
)的图像相交于点P(1,n),且C(3,2)在一次函数图像上
⑴求k、b的值;
⑵直接写出kx+b>-4x的解集
⑶连接OC,求三角形OPC的面积。
参考答案:
【答案】(1)k=3,b=-7;(2)x>1;(3)7.
【解析】
(1)把点P(1,n)代入y=-4x,得到n值,即可得到P(1,-4),把P(1,-4)和C(3,2)代入
y=kx+b中,解得k,b的值;
(2)根据图象求出P的坐标,根据图象可以看出当x>1时,一次函数y=kx+b的图象在y=-4x的上方,即可得出答案;
(3)先求出直线y=kx+b与x轴的交点,再根据三角形的面积公式计算即可.
(1)∵P(1,n)在函数y=-4x(![]() )的图象上,
)的图象上,
∴-4=n,
∴P(1,-4),
把P(1,-4)和C(3,2)代入y=kx+b中,
得![]() ,
,
解得![]() ;
;
(2)由(1)得一次函数的解析式为y=3x-7,把y=3x-7(![]() )与y=-4x图象在同一坐标系中画出,如图:
)与y=-4x图象在同一坐标系中画出,如图:

根据图象可以看出当x>1时,一次函数y=3x-7的图象在y=-4x的上方,
故3x-7>-4x的解集为:x>1;
(3)令y=0,得3x-7=0,解得x=![]() ,
,
∴M(![]() ,0),
,0),
∴S△OPC= S△OMC+ S△OMP=![]() ×
×![]() ×2+
×2+![]() ×
×![]() ×4=7.
×4=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( )
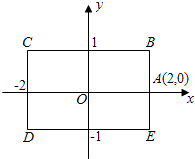
A.(2,0)
B.(﹣1,1)
C.(﹣2,1)
D.(﹣1,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中 AB=CB,AD=CD,詹姆斯在探究筝形的性质时,得到如下结论:① ACBD;②AOCO
 AC;③△ABD≌△CBD;④四边形ABCD的面积=
AC;③△ABD≌△CBD;④四边形ABCD的面积= ACBD,其中,正确的结论有_____.
ACBD,其中,正确的结论有_____.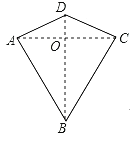
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知在△ABC中,∠C=90°,AC=5,AB=13.点D在边AC上,且点D到边AB和边BC的距离相等.
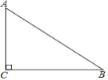
(1)用直尺圆规作出点D(不写作法,保留作图痕迹,在图上标注清楚点D);
(2)求△ABD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,BE平分∠ABD,DE平分∠BDC,且BE与DE相交于点E,求证∠E=90° 证明:∵AB∥CD()
∴∠ABD+∠BDC=180°()
∵BE平分∠ABD()
∴∠EBD= ()
()
又∵DE平分∠BDC
∴∠BDE= ()
()
∴∠EBD+∠EDB= ∠ABD+
∠ABD+  ∠BDC()
∠BDC()
= (∠ABD+∠BDC)=90°
(∠ABD+∠BDC)=90°
∴∠E=90°.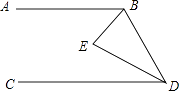
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
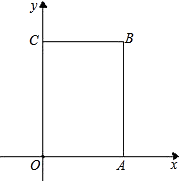
(1)写出B点的坐标();
(2)当点P移动了4秒时,描出此时P点的位置,并写出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
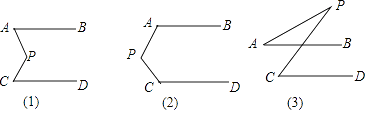
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论;
(2)当点P移动到图(2)、图(3)的位置时,∠P、∠A、∠C又有怎样的关系?请分别写出你的结论.
相关试题

