Question

【题目】如图（1），已知四边形ABCD的四条边相等，四个内角都等于90°，点E是CD边上一点，F是BC边上一点，且∠EAF=45°．

（1）求证：BF+DE=EF；

（2）若AB=6，设BF=x，DE=y，求y关于x的函数解析式，并写出x的取值范围；

（3）过点A作AH⊥FE于点H，如图（2），当FH=2，EH=1时，求△AFE的面积．

　

Answer 1

【答案】（1）见解析；（2）y=（0≤x≤6）；（3）．

【解析】

（1）如图1中，将△ADE绕点A顺时针旋转90°得到△ABH．只要证明△AFH≌△AFE（SAS）即可解决问题；,

（2）利用（1）中结论，在Rt△ECF中，根据EF2=CF2+EC2，构建关系式即可；

（3）如图2中，将△ADE绕点A顺时针旋转90°得到△ABM．首先证明AH=AB，设AB=x，在Rt△EFC中，利用勾股定理构建方程即可解决问题；

（1）如图1中，将△ADE绕点A顺时针旋转90°得到△ABH，

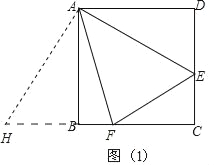
∵四边形ABCD是正方形，

∴AB=AD=CD=BC，∠BAD=90°，

∵∠EAF=45°，

∴∠BAF+∠BAH=∠BAF+∠DAE=45°，

∴∠FAH=∠FAE=45°，

∵AF=AF，AH=AE，

∴△AFH≌△AFE（SAS），

∴EF=FH，

∵FH=BH+BF=DE+BF，

∴EF=BF+DE；

（2）∵AB=BC=CD=6，BF=x，DE=y，

∴EF=x+y，FC=6=﹣x，EC=6﹣y，

在Rt△ECF中，∵EF2=CF2+EC2，

∴（x+y）2=（6﹣x）2+（6﹣y）2，

∴y=（0≤x≤6）；

（3）如图2中，将△ADE绕点A顺时针旋转90°得到△ABM．

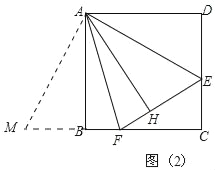
由（1）可知△AFM≌△AFH，

∵AB⊥FM，AH⊥EF，

∴AB=AH，

设AB=BC=CD=AD=x，

∵∠ABF=∠AHF=90°，

∵AF=AF．AB=AH，

∴Rt△AFB≌Rt△AFH（HL），

∴BF=FH=2，同理可证：DE=EH=1，

∴CF=x﹣2，EC=x﹣1，

在Rt△ECF中，∵EF2=CF2+EC2，

∴32=（x﹣2）2+（x﹣1）2，

∴x=或（舍弃），

∴S△AEF=EFAH=×3×=．