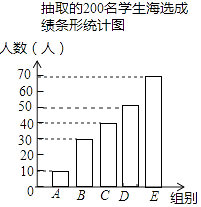
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表: 抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题: 
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 , 表示C组扇形的圆心角θ的度数为度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
参考答案:
【答案】
(1)解:D的人数是:200﹣10﹣30﹣40﹣70=50(人),
补图如下:
(2)15;72
(3)解:根据题意得:
2000× ![]() =700(人),
=700(人),
答:估计该校参加这次海选比赛的2000名学生中成绩“优等”的有700人
【解析】(2)B组人数所占的百分比是 ![]() ×100%=15%, 则a的值是15;
×100%=15%, 则a的值是15;
C组扇形的圆心角θ的度数为360× ![]() =72°;
=72°;
故答案为:15,72;
(1)用随机抽取的总人数减去A、B、C、E组的人数,求出D组的人数,从而补全统计图;(2)用B组抽查的人数除以总人数,即可求出a;用360乘以C组所占的百分比,求出C组扇形的圆心角θ的度数;(3)用该校参加这次海选比赛的总人数乘以成绩在90分以上(包括90分)所占的百分比,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.
(1)求证:BF+DE=EF;
(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.

(1)求证:AC是⊙O的切线:
(2)若BF=8,DF= ,求⊙O的半径r.
,求⊙O的半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=
 (m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n)
(m为常数,且m≠0)的图象交于点A(﹣2,1)、B(1,n) 
(1)求反比例函数与一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)直接写出当y1<y2时,自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD.
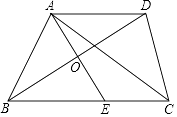
(1)求证:AO=EO;
(2)若AE是△ABC的中线,则四边形AECD是什么特殊四边形?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.

(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
相关试题

