【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)k=8;(2)15;(3) P坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).
【解析】
本题考查的是反比例函数的应用
(1)根据正比例函数先求出点A的坐标,从而求出了k值为8;
(2)根据k的几何意义,![]() ,
,![]() ;
;
(3)根据k的几何意义,![]() ,
,![]() .
.
(1)![]() 点
点![]() 横坐标为
横坐标为![]() ,
,![]() 当
当![]() 时,
时,![]() .
.![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 点
点![]() 是直线
是直线![]() 与双曲线
与双曲线![]() 的交点
的交点![]() .
.
(2)解法一:如图
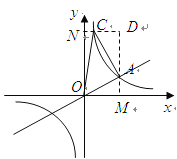
![]() 点
点![]() 在双曲线上,当
在双曲线上,当![]() 时,
时,![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
过点![]() 分别做
分别做![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,得矩形
,得矩形![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() .
.
解法二:如图
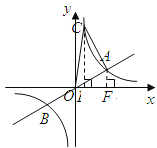
过点![]() 分别做
分别做![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,
![]() 点
点![]() 在双曲线
在双曲线![]() 上,当
上,当![]() 时,
时,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.![]() 点
点![]() ,
,![]() 都在双曲线
都在双曲线![]() 上,
上,
![]()
![]() .
.
![]() .
.![]() ,
,![]() .
.
(3)![]() 反比例函数图象是关于原点
反比例函数图象是关于原点![]() 的中心对称图形,
的中心对称图形,
![]() ,
,![]() .
.![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() .
.
设点![]() 横坐标为
横坐标为![]() ,得
,得![]() .
.
过点![]() 分别做
分别做![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,
![]() 点
点![]() 在双曲线上,
在双曲线上,![]() .
.
若![]() ,如图
,如图
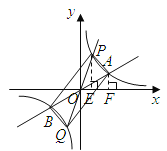
![]() ,
,
![]() .
.![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).![]()
![]() .
.
若![]() ,如图
,如图

![]() ,
,
![]() .
.![]() ,
,
解得![]() ,
,![]() (舍去).
(舍去).![]() .
.
![]() 点
点![]() 的坐标是
的坐标是![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)化简:( +
+  )÷
)÷ 
(2)解不等式组 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,∠B=15°,边AB的垂直平分线交边BC于点E,垂足为点D,取线段BE的中点F,联结DF.求证:AC=DF.(说明:此题的证明过程需要批注理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个人做游戏:在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1,2,3,4.从中随机摸出一张纸牌然后放回,再随机摸出一张纸牌,若两次摸出的纸牌上数字之和是3的倍数,则甲胜;否则乙胜.这个游戏对双方公平吗?请列表格或画树状图说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校教学楼AB的后面有一建筑物CD,在距离CD的正后方30米的观测点P处,以22°的仰角测得建筑物的顶端C恰好挡住教学楼的顶端A,而在建筑物CD上距离地面3米高的E处,测得教学楼的顶端A的仰角为45°,求教学楼AB的高度.
(参考数据:sin22°≈ ,cos22°≈
,cos22°≈  ,tan22°≈
,tan22°≈  )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.
(1)求证:BF+DE=EF;
(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.

相关试题

