【题目】问题背景(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:△EFC的面积![]() __________,△ADE的面积
__________,△ADE的面积![]() ______________.
______________.
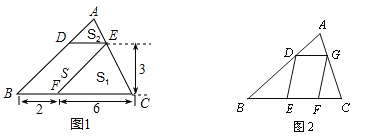
探究发现(2)在(1)中,若BF=m,FC=n,DE与BC间的距离为![]() .请证明
.请证明![]() .
.
拓展迁移(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为3、7、5,试利用(2)中的结论求△ABC的面积.
参考答案:
【答案】(1)S=6,S1=9,S2=1;(2)证明见解析;(3)27.
【解析】
试题分析:(1)四边形DBFE是平行四边形,利用底×高可求面积;△EFC的面积利用底×高的一半计算;△ADE的面积,可以先过点A作AH⊥BC,交DE于G,交BC于H,即AG是△ADE的高,AH是△ABC的高,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,利用相似三角形的面积比等于相似比的平方,可求AG,再利用三角形的面积公式计算即可;
(2)由于DE∥BC,EF∥AB,可知四边形DBFE是,同时,利用平行线分线段成比例定理的推论,可知△ADE∽△ABC,△EFC∽△ABC,从而易得△ADE∽△EFC,利用相似三角形的面积比等于相似比的平方,可得S1:S2=a2:b2,由于S1=![]() bh,那么可求S2,从而易求4S1S2,又S=ah,容易证出结论;
bh,那么可求S2,从而易求4S1S2,又S=ah,容易证出结论;
(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,容易证出△DBE≌△GHF,那么△GHC的面积等于12,再利用(2)中的结论,可求DBHG的面积,从而可求△ABC的面积.
试题解析:(1)S=6,S1=9,S2=1;
(2)∵DE∥BC,EF∥AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF,
∴△ADE∽△EFC,
∴![]() ,
,
∵S1=![]() bh,
bh,
∴S2=![]() ×S1=
×S1=![]() ,
,
∴4S1S2=4×![]() bh×
bh×![]() =(ah)2,
=(ah)2,
而S=ah,
∴S2=4S1S2;
(3)过点G作GH∥AB交BC于H,则四边形DBHG为平行四边形,
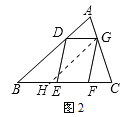
∴∠GHC=∠B,BD=HG,DG=BH,
∵四边形DEFG为平行四边形,
∴DG=EF,
∴BH=EF
∴BE=HF,
∴△DBE≌△GHF,
∴△GHC的面积为7+5=12,
由(2)得,平行四边形DBHG的面积S为![]() =12,
=12,
∴△ABC的面积为3+12+12=27.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程5x+3k=21与5x+3=0的解相同,则k的值是( )
A. -10 B. 7 C. -9 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是
A.(a+b)2=a2+b2 B.x3+x3=x6
C.(a3)2=a5 D.(2x2)(﹣3x3)=﹣6x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)某工程承包方指定由甲、乙两个工程队完成某项工程,若由甲工程队单独做需要40天完成,现在甲、乙两个工程队共同做20天后,由于甲工程队另有其他任务不再做该工程,剩下的工程由乙工程队再单独做了20天才完成任务.
(1)求乙工程队单独完成该工程需要多少天?
(2)如果工程承包方要求乙工程队的工作时间不能超过30天,要完成该工程,甲工程队至少要工作多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
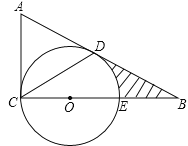
(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留
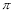 和根号).
和根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,线段EF分别交AD、AC、BC于点E、O、F,EF⊥AC,AO=CO.
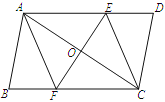
(1)求证:△AOE≌△COF;
(2)在本题的已知条件中,有一个条件如果去掉,并不影响(1)的证明,你认为这个多余的条件是 (直接写出这个条件).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若圆锥的底面半径为3,母线长为4,则这个圆锥的侧面积为( )
A. 24 B. 24π C. 12 D. 12π
相关试题

