【题目】如图,抛物线y= ![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣ ![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的解析式和tan∠BAC的值;
(2)在(1)条件下,P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】解:(1)把A(0,3),C(3,0)代入y= ![]() x2+mx+n,得
x2+mx+n,得
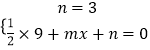 ,
,
解得: 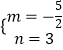 .
.
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+3.
x+3.
联立 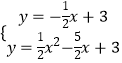 ,
,
解得: ![]() 或
或 ![]() ,
,
∴点B的坐标为(4,1).
过点B作BH⊥x轴于H,如图1.∵C(3,0),B(4,1),
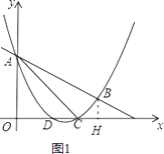
∴BH=1,OC=3,OH=4,CH=4﹣3=1,∴BH=CH=1.
∵∠BHC=90°,∴∠BCH=45°,BC= ![]() .
.
同理:∠ACO=45°,AC=3 ![]() ,
,
∴∠ACB=180°﹣45°﹣45°=90°,
∴tan∠BAC= ![]() ;
;
(2)存在点P,使得以A,P,Q为顶点的三角形与△ACB相似.
过点P作PG⊥y轴于G,
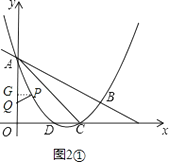
则∠PGA=90°.
设点P的横坐标为x,由P在y轴右侧可得x>0,则PG=x.
∵PQ⊥PA,∠ACB=90°,∴∠APQ=∠ACB=90°.
若点G在点A的下方,
①如图2①,当∠PAQ=∠CAB时,则△PAQ∽△CAB.
∵∠PGA=∠ACB=90°,∠PAQ=∠CAB,∴△PGA∽△BCA,
∴ ![]() .
.
∴AG=3PG=3x.
则P(x,3﹣3x).把P(x,3﹣3x)代入y= ![]() x2﹣
x2﹣ ![]() x+3,得:
x+3,得: ![]() x2﹣
x2﹣ ![]() x+3=3﹣3x,
x+3=3﹣3x,
整理得:x2+x=0,解得:x1=0(舍去),x2=﹣1(舍去).
②如图2②,
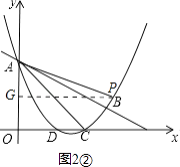
当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:AG= ![]() PG=
PG= ![]() x,则P(x,3﹣
x,则P(x,3﹣ ![]() x),
x),
把P(x,3﹣ ![]() x)代入y=
x)代入y= ![]() x2﹣
x2﹣ ![]() x+3,得:
x+3,得: ![]() x2﹣
x2﹣ ![]() x+3=3﹣
x+3=3﹣ ![]() x,
x,
整理得:x2﹣ ![]() x=0,解得:x1=0(舍去),x2=
x=0,解得:x1=0(舍去),x2= ![]() ,∴P(
,∴P( ![]() ,
, ![]() );
);
若点G在点A的上方,
①当∠PAQ=∠CAB时,则△PAQ∽△CAB,
同理可得:点P的坐标为(11,36).
②当∠PAQ=∠CBA时,则△PAQ∽△CBA.
同理可得:点P的坐标为P( ![]() ,
, ![]() ).
).
综上所述:满足条件的点P的坐标为(11,36)、( ![]() ,
, ![]() )、(
)、( ![]() ,
, ![]() ).
).
【解析】(1)将点A、B的坐标代入抛物线的解析式得到关于m、n的方程组,从而可求得m、n;过点B作BH⊥OH,先求得点C的坐标,然后再证明△AOC和△BHC为等腰直角三角形,从而可求得∠ACB=90°,然后依据勾股定理可求得AC、BC的长,最后依据锐角三角函数的定义可求得答案。
(2)过点P作PG⊥OA,当G在点A的下方时,分为∠PAQ=∠CAB和∠PAQ=∠CBA两种情况,当点G在点A的上方,分为∠PAQ=∠CAB和∠PAQ=∠CBA两情况分类计算即可..
【考点精析】通过灵活运用二次函数图象的平移和相似三角形的判定与性质,掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.

(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若 ,求⊙O的半径和线段PB的长.
,求⊙O的半径和线段PB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年1月20日,山西迎来了“复兴号”列车,与“和谐号”相比,“复兴号”列车时速更快,安全性更好.已知“太原南﹣北京西”全程大约500千米,“复兴号”G92次列车平均每小时比某列“和谐号”列车多行驶40千米,其行驶时间是该列“和谐号”列车行驶时间的
 (两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
(两列车中途停留时间均除外).经查询,“复兴号”G92次列车从太原南到北京西,中途只有石家庄一站,停留10分钟.求乘坐“复兴号”G92次列车从太原南到北京西需要多长时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,CA=12
 cm,BC=12cm;动点P从点C开始沿CA以2
cm,BC=12cm;动点P从点C开始沿CA以2  cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BC以 2cm/s的速度向点C移动.如果P、Q、R分别从C、A、B同时移动,移动时间为t(0<t<6)s.
(1)∠CAB的度数是;
(2)以CB为直径的⊙O与AB交于点M,当t为何值时,PM与⊙O相切?
(3)写出△PQR的面积S随动点移动时间t的函数关系式,并求S的最小值及相应的t值;
(4)是否存在△APQ为等腰三角形?若存在,求出相应的t值;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①△DEF是等腰直角三角形;
②AE=CF;
③△BDE≌△ADF;
④BE+CF=EF;
⑤S四边形AEDF=
 AD2,
AD2,其中正确结论是_____(填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学改革学生的学习模式,变“老师要学生学习”为“学生自主学习”,培养了学生自主学习的能力.小华与小明同学就“你最喜欢哪种学习方式”随机调查了他们周围的一些同学,根据收集到的数据绘制了以下两个不完整的统计图(如图).


请根据上面两个不完整的统计图回答以下4个问题:
(1)这次抽样调查中,共调查了_____名学生.
(2)补全条形统计图中的缺项.
(3)在扇形统计图中,选择教师传授的占_____%,选择小组合作学习的占_____%.
(4)根据调查结果,估算该校1800名学生中大约有_____人选择小组合作学习模式.
相关试题

