Question

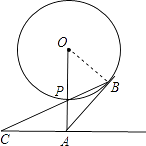
【题目】如图，已知直线l与⊙O相离，OA⊥l于点A，OA=5，OA⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C．

（1）试判断线段AB与AC的数量关系，并说明理由；
（2）若 ，求⊙O的半径和线段PB的长．

Answer 1

【答案】
（1）解：AB=AC，理由如下：

连接OB．

∵AB切⊙O于B，OA⊥AC，

∴∠OBA=∠OAC=90°，

∴∠OBP+∠ABP=90°，∠ACP+∠APC=90°，

∵OP=OB，

∴∠OBP=∠OPB，

∵∠OPB=∠APC，

∴∠ACP=∠ABC，

∴AB=AC；

（2）解：延长AP交⊙O于D，连接BD，

设圆半径为r，则OP=OB=r，PA=5﹣r，

则AB2=OA2﹣OB2=52﹣r2，

AC2=PC2﹣PA2=（2 ）2﹣（5﹣r）2，

∴52﹣r2=（2 ）2﹣（5﹣r）2，

解得：r=3，

∴AB=AC=4，

∵PD是直径，

∴∠PBD=90°=∠PAC，

又∵∠DPB=∠CPA，

∴△DPB∽△CPA，

∴ ，

∴ ，

∴BP= ，

答：圆的半径是3，线段PB的长为 ．

【解析】（1）连接OB，根据切线的性质和垂直得出∠OBA=∠OAC=90°，得出∠OBP+∠ABP=90°，∠ACP+∠CPA=90°，求出∠ACP=∠ABC，根据等腰三角形的判定推出即可。
（2）延长AP交 O于D，连接BD，设圆半径为r，则OP=OB=r，PA=5-r，根据AB=AC，建立方程求出t的值，再证明△DPB∽△CPA，得出对应边成比例，求出BP的长。